Mỗi bạn học sinh trong lớp của Minh lựa chọn học một trong hai ngoại ngữ là tiếng Anh hoặc tiếng Nhật. Xác suất chọn tiếng Anh của mỗi bạn học sinh nữ là 0,6 và của mỗi bạn học sinh nam là 0,7 . Lớp của Minh có 25 bạn nữ và 20 bạn nam. Chọn ra ngẫu nhiên một bạn trong lớp.
Sử dụng sơ đồ hình cây, tính xác suất của các biến cố:
\(A\): "Bạn được chọn là nam và học tiếng Nhật";
\(B\) : "Bạn được chọn là nữ và học tiếng Anh".
Mỗi bạn học sinh trong lớp của Minh lựa chọn học một trong hai ngoại ngữ là tiếng Anh hoặc tiếng Nhật. Xác suất chọn tiếng Anh của mỗi bạn học sinh nữ là 0,6 và của mỗi bạn học sinh nam là 0,7 . Lớp của Minh có 25 bạn nữ và 20 bạn nam. Chọn ra ngẫu nhiên một bạn trong lớp.
Sử dụng sơ đồ hình cây, tính xác suất của các biến cố:
\(A\): "Bạn được chọn là nam và học tiếng Nhật";
\(B\) : "Bạn được chọn là nữ và học tiếng Anh".
Quảng cáo
Trả lời:
Gọi M là biến cố "Bạn được chọn là nữ";
N là biến cố "Bạn được chọn học tiếng Anh".
Ta có \(P(M) = \frac{{C_{\frac{1}{1}}^{C_{45}^1}}}{{C_{45}^1}}\frac{5}{9};P(N\mid M) = 0,6;P(N\mid \bar M) = 0,7\).
Suy ra \(P(\bar M) = 1 - P(M) = \frac{4}{9};P(\bar N\mid M) = 1 - P(N\mid M) = 0,4\); \(P(\bar N\mid \bar M) = 1 - P(N\mid \bar M) = 0,3\).
Ta có sơ đồ hình cây
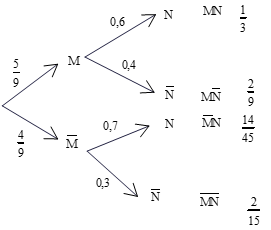
Dựa vào sơ đồ hình cây, ta có: \(P(A) = \frac{2}{{15}};P(B) = \frac{1}{3}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(A\) là biến cố "Kiện hành lí có chứa hàng cấm" và \(B\) là biến cố "Máy phát chuông cảnh báo". Ta có
\(P(B\mid A) = 0,95;P(B\mid \bar A) = 0,02;P(A) = 0,001.\)
Do đó \(P(\bar A) = 1 - P(A) = 0,999;P(\bar B\mid A) = 1 - P(B\mid A) = 0,05;P(\bar B\mid \bar A) = 1 - P(B\mid \bar A) = 0,98\).
Ta có sơ đồ hình cây như sau:
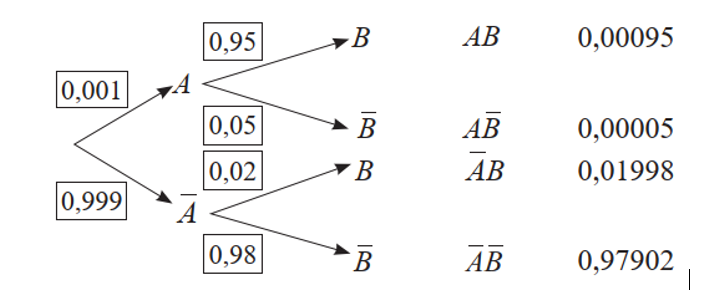
Do \(M = AB\) nên \(P(M) = P(AB) = 0,00095\).
Do \(N = \bar AB\) nên \(P(N) = P(\bar AB) = 0,01998\).
Lời giải
Gọi A là biến cố "UPS bị hỏng khi xảy ra sự cố điện".
B là biến cố "Máy tính bị hỏng".
Ta có \({\rm{P}}({\rm{A}}) = 0,02;{\rm{P}}({\rm{B}}\mid {\rm{A}}) = 0,1;P(\bar B\mid \bar A) = 1\).
Suy ra \(P(\bar B\mid A) = 1 - P(B\mid A) = 0,9\).
Ta có sơ đồ cây như sau:
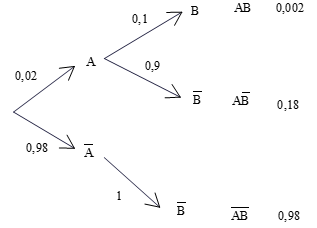
Dựa vào sơ đồ cây ta có:
\(P(AB) = 0,002\).Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.