Trong không gian Oyz cho hai mặt phẳng (P):x-3y+2z-1=0, (Q):x-z+2=0 . Mặt phẳng ($\alpha$) vuông góc với cả (P) và (Q) đồng thời cắt trục Ox tại điểm có hoành độ bằng 3 Phương trình của mp ($\alpha$)  là

Trong không gian \[Oxyz\], cho mặt phẳng ba mặt phẳng \(\left( P \right):x + y + z - 1 = 0\), \(\left( Q \right):2x + my + 2z + 3 = 0\) và \(\left( R \right): - x + 2y + nz = 0\). Tính tổng \(m + 2n\), biết rằng \(\left( P \right) \bot \left( R \right)\) và \(\left( P \right)//\left( Q \right)\)

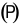Trong không gian với hệ tọa độ Oyz, cho hai điểm $A(0;1;1)$) và $B(1;2;3)$. Viết phương trình của mặt phẳng đi qua A và vuông góc với đường thẳng AB.

Trong không gian với hệ tọa độ \(Oxyz\), cho hai mặt phẳng \(\left( P \right):2x + my + 3z - 5 = 0\) và\(\left( Q \right):nx - 8y - 6z + 2 = 0\), với \(m,n \in \mathbb{R}\). Xác định \(m,n\) để \(\left( P \right)\)song song với \(\left( Q \right)\).

Trong không gian Oyz, mặt phẳng (P) đi qua hai điểm A(0;1;0),B(2;3;1) và vuông góc với mặt phẳng $\left(Q\right):x+2y-z=0$ có phương trình là

Trong không gian \(Oxyz\), mặt phẳng \(\left( P \right):2x + y + z - 2 = 0\) vuông góc với mặt phẳng nào dưới đây?

Trong không gian \[Oxyz\], cho mặt phẳng \(\left( P \right):2x - y + 2z - 4 = 0\). Gọi \(H\) là hình chiếu vuông góc của điểm \(M\left( {3\,;\,1\,;\, - 2} \right)\) lên mặt phẳng \(\left( P \right)\). Độ dài đoạn thẳng \(MH\) là

Trong không gian với hệ trục tọa độ \(Oxyz\), gọi \(H\) là hình chiếu vuông góc của điểm \[A\left( {1; - 2;3} \right)\] lên mặt phẳng \(\left( P \right):2x - y - 2z + 5 = 0\). Độ dài đoạn thẳng \(AH\) là