PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S)
Cho hàm số \[y = f\left( x \right) = \frac{{a{x^2} + bx + 1}}{{cx + d}}\] đạt cực đại tại \[x = 0\] và có đồ thị như hình vẽ sau:
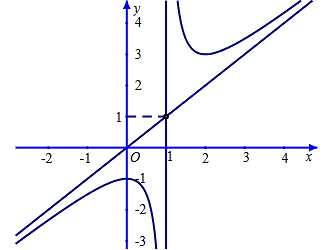
a) Giá trị của biểu thức \[a + b + c + d = 0.\]
b) Hàm số đồng biến trên \[\left( { - 1;0} \right).\]
c) Gọi \[A,B\] là các điểm cực trị của đồ thị hàm số; \[M\] là điểm di động trên trục \[Ox\] sao cho \[\widehat {AMB}\] không tù. Giá trị nhỏ nhất của hoành độ điểm \[M\] là 3.
d) Đường thẳng đi qua hai điểm cực trị của hàm số có phương trình: \[y = x - 1.\]
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng (Đ) hoặc sai (S)
Cho hàm số \[y = f\left( x \right) = \frac{{a{x^2} + bx + 1}}{{cx + d}}\] đạt cực đại tại \[x = 0\] và có đồ thị như hình vẽ sau:

a) Giá trị của biểu thức \[a + b + c + d = 0.\]
b) Hàm số đồng biến trên \[\left( { - 1;0} \right).\]
c) Gọi \[A,B\] là các điểm cực trị của đồ thị hàm số; \[M\] là điểm di động trên trục \[Ox\] sao cho \[\widehat {AMB}\] không tù. Giá trị nhỏ nhất của hoành độ điểm \[M\] là 3.
d) Đường thẳng đi qua hai điểm cực trị của hàm số có phương trình: \[y = x - 1.\]
Câu hỏi trong đề: Bộ 3 đề KSCL đầu năm Toán 12 có đáp án !!
Quảng cáo
Trả lời:
a) Đúng. Xét hàm số có đồ thị \[y = f\left( x \right) = \frac{{a{x^2} + bx + 1}}{{cx + d}}\] nhận đường \[x = 1\] làm tiệm cận đứng và cắt trục tung tại điểm \[\left( {0; - 1} \right)\] nên ta có: \[\left\{ \begin{array}{l}c + d = 0\\\frac{1}{d} = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 1\\d = - 1\end{array} \right..\]
Đồ thị hàm số có đường tiệm cận xiên \[y = x\].
Ta có \[y = f\left( x \right) = \frac{{a{x^2} + bx + 1}}{{x - 1}} = ax + b + a + \frac{{a + b + 1}}{{x - 1}}\].
Nên tiệm cận xiên là đường \[y = ax + b + a \Rightarrow \left\{ \begin{array}{l}a = 1\\b + a = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = - 1\end{array} \right.\].
Do đó ta có \[a + b + c + d = 1 - 1 + 1 - 1 = 0.\]
b) Đúng. Từ đồ thị ta nhận thấy trên khoảng \[\left( { - 1;0} \right)\] đồ thị hàm số là đường liền nét đi lên từ trái qua phải nên hàm số đồng biến trên \[\left( { - 1;0} \right).\]
c) Sai. Ta có \[y = f\left( x \right) = x + \frac{1}{{x - 1}} \Rightarrow f'\left( x \right) = 1 - \frac{1}{{{{\left( {x - 1} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right..\]
\[f\left( 0 \right) = - 1;f\left( 2 \right) = 3 \Rightarrow A\left( {0; - 1} \right);B\left( {2;3} \right).\]
Gọi \[M\left( {t;0} \right) \in Ox\]. Khi góc \[AMB\] không tù thì \[\overrightarrow {MA} \cdot \overrightarrow {MB} \ge 0.\]
\[\overrightarrow {MA} = \left( { - t; - 1} \right);\overrightarrow {MB} = \left( {2 - t;3} \right) \Rightarrow - t\left( {2 - t} \right) - 3 \ge 0 \Leftrightarrow {t^2} - 2t - 3 \ge 0 \Leftrightarrow \left[ \begin{array}{l}t \ge 3\\t \le - 1\end{array} \right..\]
d) Sai. Đồ thị hàm số có 2 điểm cực trị là: \[A\left( {0; - 1} \right);B\left( {2;3} \right).\]
Đường thẳng \[y = x - 1\] không đi qua \[B\left( {2;3} \right).\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x\,\,\left( {0 < x \le 14} \right)\) là số máy in cần sử dụng để in lô hàng.
Chi phí cài đặt là \(12x\).
Số giờ in hết số ấn phẩm là \(\frac{{4000}}{{30x}}\) (giờ), chi phí giám sát là \(\frac{{4000}}{{30x}} \cdot 9 = \frac{{1200}}{x}\) (USD).
Tổng chi phí in là \(P\left( x \right) = 12x + \frac{{1200}}{x}\) .
\(P'\left( x \right) = 12 - \frac{{1200}}{{{x^2}}}\)
\(P'\left( x \right) = 0 \Leftrightarrow {x^2} = 100 \Leftrightarrow \left[ \begin{array}{l}x = 10\\x = - 10\,\,\left( L \right)\end{array} \right.\).
Bảng biến thiên:
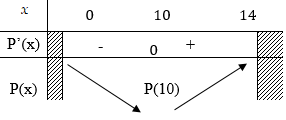
Vậy để chi phí in nhỏ nhất thì số máy phải sử dụng là \(10\) máy.
Đáp án: \(10\).
Câu 2
A. \({a^2}\).
B. \({a^2}\sqrt 2 \).
C. \( - {a^2}\).
D. \(\frac{{{a^2}\sqrt 2 }}{2}\).
Lời giải
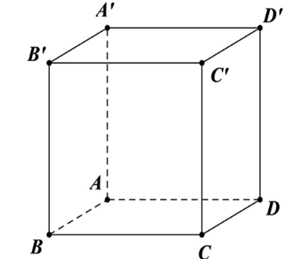
Ta có \(\overrightarrow {BC'} \cdot \overrightarrow {B'A} = \overrightarrow {AD'} \cdot \overrightarrow {B'A} = - \overrightarrow {AD'} .\overrightarrow {AB'} = - a\sqrt 2 \cdot a\sqrt 2 \cdot \cos \left( {\overrightarrow {AD'} ,\overrightarrow {AB'} } \right) = - {a^2}\). Chọn C.
Câu 3
A. \(M\left( {1;1;0} \right)\).
B. \(M\left( {3; - 4;5} \right)\).
C. \(M\left( { - 3;5;0} \right)\).
D. \(M\left( { - 2;1;0} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.\(\mathop {{\rm{max}}}\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( 0 \right)\).
B. \(\mathop {{\rm{max}}}\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( 3 \right)\).
C. \(\mathop {{\rm{max}}}\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( 2 \right)\).
D. \(\mathop {{\rm{max}}}\limits_{\left[ { - 1;3} \right]} f\left( x \right) = f\left( { - 1} \right)\) .
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(M\left( {1;\,2} \right)\).
B. \(Q\left( {1;\, - 3} \right)\).
C. \(N\left( {3;\,1} \right)\).
D. \(P\left( {2;\,2} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho hàm số y = f( x ) liên tục và có bảng biến thiên trên đoạn [- 1;3] như hình vẽ bên.Khẳng định nào sau đây đúng? (ảnh 1)](https://video.vietjack.com/upload2/images/1754821452/1754821529-image5.png)