Trong mặt phẳng \(Oxy\), cho đường tròn \(\left( C \right)\) có phương trình \(\,{x^2} + {y^2} - 6x + 2y + 6 = 0\). Tọa độ tâm \(I\) của đường tròn \(\left( C \right)\) là
Câu hỏi trong đề: Bộ 3 đề KSCL đầu năm Toán 11 có đáp án !!
Quảng cáo
Trả lời:
Đường tròn \(\left( C \right)\) có phương trình \(\,{x^2} + {y^2} - 6x + 2y + 6 = 0 \Leftrightarrow {\left( {x - 3} \right)^2} + {\left( {y + 1} \right)^2} = 4\).
Suy ra tâm của đường tròn là \(I\left( {3; - 1} \right)\). Chọn D.
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
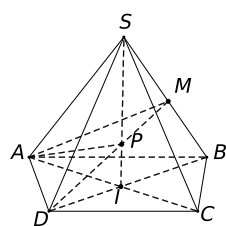
Ta có \(P = MD \cap SI\). Khi đó, \(\left\{ \begin{array}{l}P \in MD,MD \subset \left( {ADM} \right)\\P \in SI,SI \subset \left( {SAC} \right)\end{array} \right. \Rightarrow P \in \left( {ADM} \right) \cap \left( {SAC} \right).\)
Ngoài ra \(A \in \left( {ADM} \right) \cap \left( {SAC} \right)\), do đó \(\left( {ADM} \right) \cap \left( {SAC} \right) = AP.\)Chọn C.
Lời giải
Đáp án
Ta có \(\frac{1}{{{{\sin }^2}\alpha }} = 1 + {\cot ^2}\alpha = 1 + 18 = 19\)\( \Rightarrow {\sin ^2}\alpha = \frac{1}{{19}}\)\( \Rightarrow \sin \alpha = \pm \frac{1}{{\sqrt {19} }}\).
Vì \[\frac{\pi }{2} < \alpha < \pi \]\[ \Rightarrow \sin \alpha > 0\]\[ \Rightarrow \sin \alpha = \frac{1}{{\sqrt {19} }}\].</>
Suy ra \[\tan \frac{\alpha }{2} + \cot \frac{\alpha }{2} = \frac{{{{\sin }^2}\frac{\alpha }{2} + {{\cos }^2}\frac{\alpha }{2}}}{{\sin \frac{\alpha }{2}\cos \frac{\alpha }{2}}} = \frac{2}{{\sin \alpha }} = 2\sqrt {19} \approx 8,72\].
Đáp án: \[8,72\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.