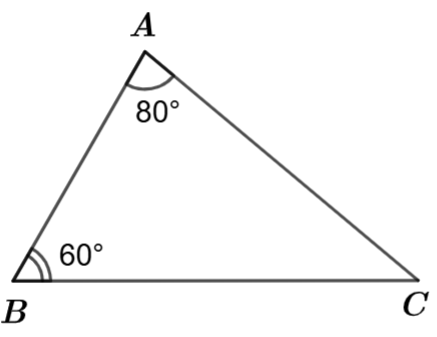
Cho tam giác \[ABC\] có số đo \(\widehat A,\,\,\widehat B,\,\,\widehat C\) theo thứ tự là \[80^\circ ;{\rm{ }}60^\circ ;{\rm{ }}40^\circ .\] Khẳng định nào sau đây là đúng?
A. \(BC > AC > AB.\)
B. \(BC < AC < AB.\)
</>
C. \[BC > AB > AC.\]
D. \(AB < BC < AC.\)
</>
Câu hỏi trong đề: Bộ 3 đề KSCL đầu năm Toán 8 có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: A
Ta có \(\widehat A = 80^\circ ,\,\,\widehat B = 60^\circ ,\,\,\widehat C = 40^\circ .\)
Cạnh đối diện với các góc \(\widehat A,\,\,\widehat B,\,\,\widehat C\) lần lượt là \(BC,\,\,AC,\,\,AB.\)
Vì \(\widehat A > \widehat B > \widehat C\) nên \(BC > AC > AB.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
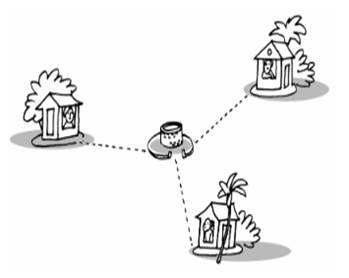
Gọi vị trí ba ngôi nhà lần lượt là \[A,{\rm{ }}B,{\rm{ }}C,\] vị trí giếng cần đào là \[O.\]
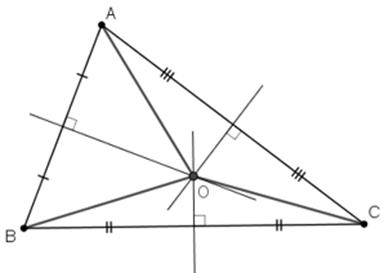
Vì điểm \[O\] cách đều ba điểm \[A,{\rm{ }}B,{\rm{ }}C\] nên O là giao điểm của ba đường trung trực của tam giác \[ABC.\]
Vậy để khoảng cách từ giếng đến các nhà bằng nhau thì vị trí của giếng ở giao ba đường trung trực của tam giác chứa ba cạnh nối liền ba ngôi nhà.
Lời giải
a) Nếu lớp 8A mỗi bạn ủng hộ 5 quyển vở thì tổng số vở lớp 8A quyên góc được là:
\[41 \cdot 5 = 205\] (quyển vở).
b) Biểu thức đại số biểu thị tổng số vở quyên góc được của 2 lớp 8A và 8B là: \[41x + 44y\] (quyển vở)
c) Nếu lớp 8A mỗi bạn ủng hộ 5 quyển và lớp 8B mỗi bạn ủng hộ được 4 quyển thì tổng số vở quyên góp được là: \[41 \cdot 5 + 44 \cdot 4 = 381\] (quyển vở).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\frac{1}{3}\).
B. \(\frac{1}{6}\).
C. \(\frac{2}{3}\).
D. \(\frac{1}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \[\frac{{a + h}}{2}\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].
B. \[\frac{{a \cdot h}}{2}\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].
C. \[a + h\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].
D. \[a \cdot h\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(2{y^2} - 6y.\)
B. \(6y{\rm{.}}\)
C. \( - 2y{\rm{.}}\)
D. \(2y{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.