Phần II. Tự luận (7,0 điểm)
(1,5 điểm) Ngày 10 tháng 9 năm 2024 Liên đội trường THCS A phát động quyên góp sách vở đồ dùng học tập để ủng hộ học sinh vùng lũ. Lớp 8A có 41 học sinh mỗi học sinh ủng hộ \[x\] quyển vở, lớp 8B có 44 học sinh mỗi học sinh ủng hộ \[y\] quyển vở.
a) Nếu lớp 8A mỗi bạn ủng hộ 5 quyển vở thì tổng số vở lớp 8A quyên góp là bao nhiêu?
b) Viết biểu thức đại số biểu thị tổng số vở quyên góp của hai lớp 8A và 8B.
c) Tính tổng số vở quyên góp được của cả hai lớp nếu lớp 8A mỗi bạn ủng hộ 5 quyển và lớp 8B mỗi bạn ủng hộ được 4 quyển.
Phần II. Tự luận (7,0 điểm)
(1,5 điểm) Ngày 10 tháng 9 năm 2024 Liên đội trường THCS A phát động quyên góp sách vở đồ dùng học tập để ủng hộ học sinh vùng lũ. Lớp 8A có 41 học sinh mỗi học sinh ủng hộ \[x\] quyển vở, lớp 8B có 44 học sinh mỗi học sinh ủng hộ \[y\] quyển vở.
a) Nếu lớp 8A mỗi bạn ủng hộ 5 quyển vở thì tổng số vở lớp 8A quyên góp là bao nhiêu?
b) Viết biểu thức đại số biểu thị tổng số vở quyên góp của hai lớp 8A và 8B.
c) Tính tổng số vở quyên góp được của cả hai lớp nếu lớp 8A mỗi bạn ủng hộ 5 quyển và lớp 8B mỗi bạn ủng hộ được 4 quyển.
Câu hỏi trong đề: Bộ 3 đề KSCL đầu năm Toán 8 có đáp án !!
Quảng cáo
Trả lời:
a) Nếu lớp 8A mỗi bạn ủng hộ 5 quyển vở thì tổng số vở lớp 8A quyên góc được là:
\[41 \cdot 5 = 205\] (quyển vở).
b) Biểu thức đại số biểu thị tổng số vở quyên góc được của 2 lớp 8A và 8B là: \[41x + 44y\] (quyển vở)
c) Nếu lớp 8A mỗi bạn ủng hộ 5 quyển và lớp 8B mỗi bạn ủng hộ được 4 quyển thì tổng số vở quyên góp được là: \[41 \cdot 5 + 44 \cdot 4 = 381\] (quyển vở).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(BC > AC > AB.\)
B. \(BC < AC < AB.\)
</>
C. \[BC > AB > AC.\]
D. \(AB < BC < AC.\)
</>
Lời giải
Đáp án đúng là: A
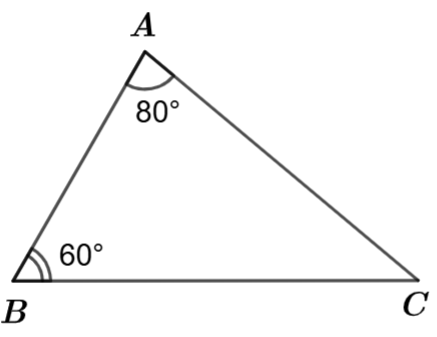
Ta có \(\widehat A = 80^\circ ,\,\,\widehat B = 60^\circ ,\,\,\widehat C = 40^\circ .\)
Cạnh đối diện với các góc \(\widehat A,\,\,\widehat B,\,\,\widehat C\) lần lượt là \(BC,\,\,AC,\,\,AB.\)
Vì \(\widehat A > \widehat B > \widehat C\) nên \(BC > AC > AB.\)
Lời giải
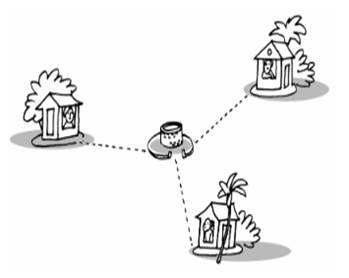
Gọi vị trí ba ngôi nhà lần lượt là \[A,{\rm{ }}B,{\rm{ }}C,\] vị trí giếng cần đào là \[O.\]
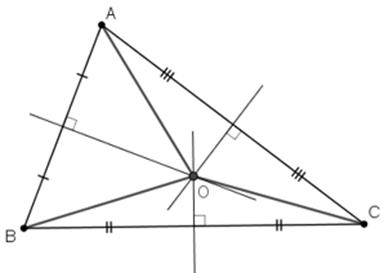
Vì điểm \[O\] cách đều ba điểm \[A,{\rm{ }}B,{\rm{ }}C\] nên O là giao điểm của ba đường trung trực của tam giác \[ABC.\]
Vậy để khoảng cách từ giếng đến các nhà bằng nhau thì vị trí của giếng ở giao ba đường trung trực của tam giác chứa ba cạnh nối liền ba ngôi nhà.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \[\frac{{a + h}}{2}\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].
B. \[\frac{{a \cdot h}}{2}\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].
C. \[a + h\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].
D. \[a \cdot h\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(\frac{1}{3}\).
B. \(\frac{1}{6}\).
C. \(\frac{2}{3}\).
D. \(\frac{1}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(2{y^2} - 6y.\)
B. \(6y{\rm{.}}\)
C. \( - 2y{\rm{.}}\)
D. \(2y{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.