Cho \[\Delta ABC\] nhọn \[\left( {AB < AC} \right),\] ba đường cao \[AE,\,\,BD,\,\,CF\] cắt nhau tại \[H.\]
a) Chứng minh:
b) Chứng minh: \[AB \cdot DF = AD \cdot BC.\]
c) Chứng minh: \[BH \cdot BD + CH \cdot CF = B{C^2}\] và \(\frac{{HE}}{{AE}} + \frac{{HD}}{{BD}} + \frac{{HF}}{{CF}} = 1.\)
Cho \[\Delta ABC\] nhọn \[\left( {AB < AC} \right),\] ba đường cao \[AE,\,\,BD,\,\,CF\] cắt nhau tại \[H.\]
a) Chứng minh:
b) Chứng minh: \[AB \cdot DF = AD \cdot BC.\]
c) Chứng minh: \[BH \cdot BD + CH \cdot CF = B{C^2}\] và \(\frac{{HE}}{{AE}} + \frac{{HD}}{{BD}} + \frac{{HF}}{{CF}} = 1.\)
Câu hỏi trong đề: Bộ 3 đề KSCL đầu năm Toán 9 có đáp án !!
Quảng cáo
Trả lời:
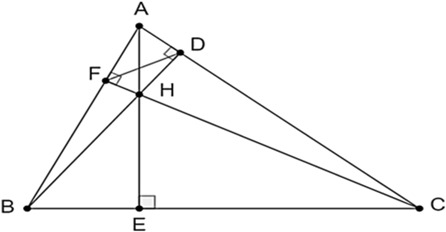
a) Vì \[H\] là giao điểm của ba đường cao \[AE,\,\,BD,\,\,CF\] nên \[H\] là trực tâm của \[\Delta ABC\]
Xét \[\Delta ABD\] và \[\Delta ACF\] có:
\[\widehat {BAD}\] chung; \[\widehat {ADB} = \widehat {AFC} = 90^\circ \].
Do đó
b) Ta có (câu a) suy ra \(\frac{{AD}}{{AB}} = \frac{{AF}}{{AC}}.\)
• Xét \[\Delta ABC\] và \[\Delta ADF\] có:
\[\widehat {BAC}\] chung; \(\frac{{AD}}{{AB}} = \frac{{AF}}{{AC}}.\)
Do đó
Suy ra \(\frac{{AB}}{{AD}} = \frac{{BC}}{{DF}}\) hay \[AB \cdot DF = AD \cdot BC\] (đpcm).
• Xét \[\Delta BEH\] và \[\Delta BDC\] có:
\(\widehat {EBH}\) chung; \(\widehat {BEH} = \widehat {BDC} = 90^\circ .\)
Do đó
Suy ra \(\frac{{BE}}{{BD}} = \frac{{BH}}{{BC}}\) hay \[BH \cdot BD = BE \cdot BC\]. (1)
Tương tự: \[CH \cdot CF = CE \cdot CB\]. (2)
Từ (1) và (2) ta có: \[BH \cdot BD + CH \cdot CF = BE \cdot BC + CE \cdot BC\]
\[ = BC\left( {BE + CE} \right) = BC \cdot BC = B{C^2}\]. (đpcm).
Mặt khác: \[\frac{{HE}}{{AE}} + \frac{{HD}}{{BD}} + \frac{{HF}}{{CF}}\]
\[ = \frac{{\frac{1}{2} \cdot HE \cdot BC}}{{\frac{1}{2} \cdot AE \cdot BC}} + \frac{{\frac{1}{2} \cdot HD \cdot AC}}{{\frac{1}{2} \cdot BD \cdot AC}} + \frac{{\frac{1}{2} \cdot HF \cdot AB}}{{\frac{1}{2} \cdot CF \cdot AB}}\]
\[ = \frac{{{S_{HBC}}}}{{{S_{ABC}}}} + \frac{{{S_{HAC}}}}{{{S_{BAC}}}} + \frac{{{S_{HAB}}}}{{{S_{CAB}}}}\]
\[ = \frac{{{S_{HBC}} + {S_{HAC}} + {S_{HAB}}}}{{{S_{ABC}}}} = \frac{{{S_{ABC}}}}{{{S_{ABC}}}} = 1.\] (đpcm)
Vậy \[BH \cdot BD + CH \cdot CF = B{C^2}\] và \(\frac{{HE}}{{AE}} + \frac{{HD}}{{BD}} + \frac{{HF}}{{CF}} = 1.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chu vi đáy của hộp quà là: \[6 \cdot 4 = 24\,\,({\rm{cm}}).\]
Diện tích xung quanh của hộp quà là: \[{S_{xq}} = \frac{1}{2} \cdot 24 \cdot 5 = 60\,\,({\rm{c}}{{\rm{m}}^2}).\]
Vậy diện tích xung quanh của hộp quà là \[60\,\,{\rm{c}}{{\rm{m}}^2}.\]
Lời giải
Ta có \[D = 2{x^2} + {y^2} - 6x + 2xy - 2y + 7\]
\[ = \frac{1}{2}\left( {4{x^2} + 2{y^2} - 12x + 4xy - 4y + 14} \right)\]
\[ = \frac{1}{2}\left[ {\left( {{y^2} + 2y + 1} \right) + \left( {4{x^2} + {y^2} + 9 + 4xy - 12x - 6y} \right)} \right] + 2\]
\[ = \frac{1}{2}\left[ {{{\left( {y + 1} \right)}^2} + {{\left( {2x + y - 3} \right)}^2}} \right] + 2 \ge 2\].
Dấu “=” xảy ra khi và chỉ khi \(x = 2\,;\,\,y = - 1.\)
Vậy giá trị nhỏ nhất của biểu thức \(D\) là 2 khi \(x = 2\,;\,\,y = - 1.\)
Câu 3
A. \(2{x^2} - 1.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
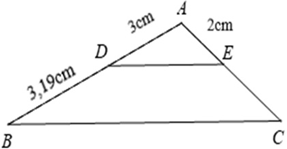
A. \[2,13\,\,{\rm{cm}}.\]
B. \[2,15\,\,{\rm{cm}}.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \[a = 2.\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.