Đồ thị nào sau đây biểu diễn mối quan hệ giữa khối lượng nước còn lại trong bình nhiệt lượng kế và thời gian của quá trình hoá hơi của nước?
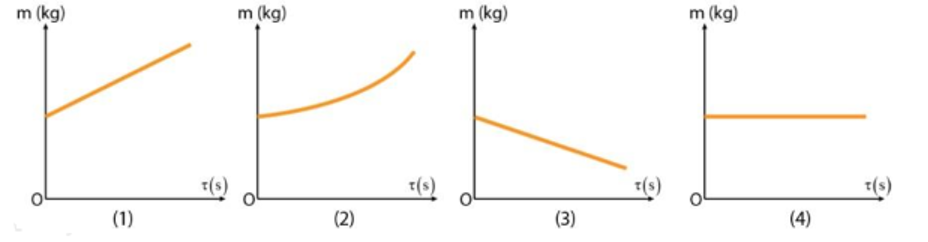
Đồ thị nào sau đây biểu diễn mối quan hệ giữa khối lượng nước còn lại trong bình nhiệt lượng kế và thời gian của quá trình hoá hơi của nước?

Quảng cáo
Trả lời:
Phương pháp:
Lý thuyết về quá trình hóa hơi.
Cách giải:
Đối với quá trình hóa hơi, theo thời gian khối lượng nước giảm.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- 500 Bài tập tổng ôn Vật lí (Form 2025) ( 38.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp:
+ Nhớ lại quy ước dấu và định luật I nhiệt động lực học: \({\rm{\Delta }}U = Q + A\).
+ Công của khối khí: \(A = p.{\rm{\Delta }}V\)
Cách giải:
+ Truyền nhiệt lượng cho Q cho khối khí nén \({\rm{Q}} > 0\)
\( \to \) b sai.
+ Độ lớn công của khối khí thực hiện là:
\(\left| A \right| = p{\rm{\Delta }}V = {3.10^5}{.7.10^{ - 3}} = 2100\left( J \right)\)
\( \to \) c đúng.
Áp dụng định luật I nhiệt động lực học:
\({\rm{\Delta }}U = Q + A \Rightarrow - 1100 = Q - 2100 \Rightarrow Q = 1000\left( J \right)\)
\( \to \) a đúng.
+ Thể tích của khối khí tăng thêm 7,0 lít
Lời giải
Phương pháp:
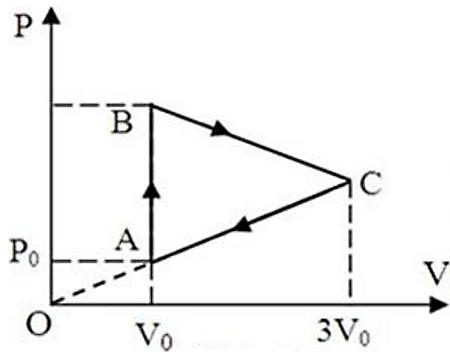
- Với \(\frac{{pV}}{T} = \) const \( \Rightarrow {T_{{\rm{max\;}}}}\) thì \({({\rm{pV}})_{{\rm{max\;}}}}\) nên trạng thái đó nằm trên đoạn BC.
- Theo đầu bài, \({T_B} = {T_C}\) thì \({T_{{\rm{max\;}}}}\) sẽ ở trung điểm của \(BC\).
- Áp dụng phương trình trạng thái khí tìm \({{\rm{T}}_{{\rm{max\;}}}}\)
Cách giải:
Với \(\frac{{pV}}{T} = \)const\( \Rightarrow {T_{{\rm{max}}}}\) thì \({({\rm{pV}})_{{\rm{max}}}}\) nên trạng thái đó nằm trên đoạn BC.
Theo Talet có:
\({p_c} = 3{p_0}\) và \({T_B} = {T_C} \Rightarrow {p_B}{V_B} = {p_C}{V_C}\)
\( \Rightarrow {p_B}.{V_0} = 3{p_0}.3{V_0} \Rightarrow {p_B} = 9{p_0}\)
Ta có: \({T_B} = {T_C}\) thì \({T_{{\rm{max\;}}}}\) sẽ ở trung điểm của \(BC\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{V = \frac{{{V_B} + {V_C}}}{2} = \frac{{{V_0} + 3{V_0}}}{2} = 2{V_0}}\\{p = \frac{{{p_B} + {p_C}}}{2} = \frac{{3{p_0} + 9{p_0}}}{2} = 6{p_0}}\end{array}} \right.\)
Phương trình trạng thái khí:
\(\frac{{pV}}{T} = \frac{{{p_0}{V_0}}}{{{T_0}}} \Rightarrow \frac{{6{p_0}2{V_0}}}{{{T_{{\rm{max}}}}}} = \frac{{{p_0}{V_0}}}{{250}}\)
\( \Rightarrow {T_{{\rm{max\;}}}} = 3000\left( {\rm{K}} \right)\)
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.