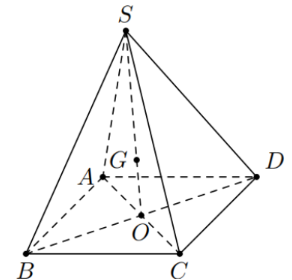
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành tâm \(O\). \(G\) là điểm thỏa mãn \(\overrightarrow {GS} + \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \).
a) \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \overrightarrow {SO} \).
b) \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \).
c) \(\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \).
d) \(\overrightarrow {GS} = 3\overrightarrow {OG} \).
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành tâm \(O\). \(G\) là điểm thỏa mãn \(\overrightarrow {GS} + \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \).

a) \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \overrightarrow {SO} \).
b) \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \).
c) \(\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \).
d) \(\overrightarrow {GS} = 3\overrightarrow {OG} \).
Quảng cáo
Trả lời:
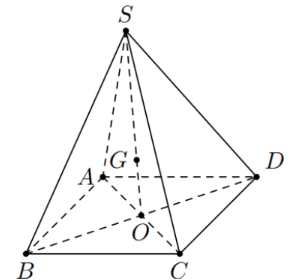
a) Sai. Ta có: \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \overrightarrow {AA} = \overrightarrow 0 \).
b) Đúng. Vì \(O\) là tâm hình bình hành \(ABCD\) nên \(O\) là trung điểm của \(AC\) và \(BD\).
Khi đó, \(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow 0 ;\,\,\overrightarrow {OB} + \overrightarrow {OD} = \overrightarrow 0 \), suy ra \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \).
c) Đúng. Ta có \(\left\{ \begin{array}{l}\overrightarrow {SB} + \overrightarrow {SD} = 2\overrightarrow {SO} \\\overrightarrow {SA} + \overrightarrow {SC} = 2\overrightarrow {SO} \end{array} \right.\), do đó \(\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \).
d) Sai. Ta có \(\overrightarrow {GS} + \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {GS} + \left( {\overrightarrow {GO} + \overrightarrow {OA} } \right) + \left( {\overrightarrow {GO} + \overrightarrow {OB} } \right) + \left( {\overrightarrow {GO} + \overrightarrow {OC} } \right) + \left( {\overrightarrow {GO} + \overrightarrow {OD} } \right) = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {GS} + 4\overrightarrow {GO} + \left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} } \right) = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {GS} + 4\overrightarrow {GO} = \overrightarrow 0 \)\( \Leftrightarrow \overrightarrow {GS} = 4\overrightarrow {OG} \).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
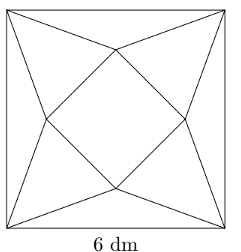
Gọi chiều rộng của đáy bể bơi là \(x,\,x > 0.\) Suy ra, chiều dài của đáy bể bơi là \(3x.\)
\(h\) là chiều cao của bể bơi \(\left( {h > 0} \right).\)
Theo giả thiết: \(V = 150 \Leftrightarrow h \cdot 3{x^2} = 150 \Leftrightarrow h = \frac{{150}}{{3{x^2}}} = \frac{{50}}{{{x^2}}}.\)
Diện tích các mặt bên và mặt đáy bể bơi là: \(S = 2hx + 6hx + 3{x^2} = 8hx + 3{x^2} = \frac{{400}}{x} + 3{x^2}\).
Ta có: \(S' = - \frac{{400}}{{{x^2}}} + 6x = \frac{{6{x^3} - 400}}{{{x^2}}}\); \(S' = 0 \Leftrightarrow x = \sqrt[3]{{\frac{{400}}{6}}} \approx 4,05\).
Lập BBT suy ra S đạt GTNN khi \(x = 4,05{\rm{ m}}{\rm{.}}\)
Vậy chiều rộng của đáy bể bơi là \(x = 4,05{\rm{ m}}\) để khi thi công tiết kiệm nguyên vật liệu nhất.
Đáp án: 4,05.
Lời giải
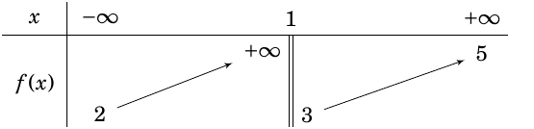
Ta có \(\mathop {\lim }\limits_{x \to {{\left( {\frac{1}{2}} \right)}^ + }} \frac{{{x^2} - 3x + 1}}{{2x - 1}} = - \infty \), suy ra đường thẳng \(x = \frac{1}{2}\) là tiệm cận đứng của đồ thị hàm số \(y = f\left( x \right)\).
Ta có \(a = \mathop {\lim }\limits_{x \to + \infty } \frac{{f\left( x \right)}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} - 3x + 1}}{{2{x^2} - x}} = \frac{1}{2}\);
\(b = \mathop {\lim }\limits_{x \to + \infty } \left( {f\left( x \right) - ax} \right) = \mathop {\lim }\limits_{x \to + \infty } \left( {\frac{{{x^2} - 3x + 1}}{{2x - 1}} - \frac{1}{2}x} \right) = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 5x + 2}}{{4x - 2}} = - \frac{5}{4}\).
Suy ra đường thẳng \(y = \frac{1}{2}x - \frac{5}{4}\) là tiệm cận xiên của đồ thị hàm số \(y = f\left( x \right)\).
Vậy điểm \(I\left( {\frac{1}{2};\, - 1} \right)\), khi đó \(\frac{1}{2} + \left( { - 1} \right) = - \frac{1}{2} = - 0,5\).
Đáp án: \( - 0,5\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.