Một chiếc xe bán tải chạy trên đường cao tốc Bắc - Nam hướng đi từ Hà Nội đến Thành phố Hồ Chí Minh trong một ngày mùa hè. Xe đi vào sáng sớm với nhiệt độ ngoài trời là \({27^ \circ }{\rm{C}}\). Thể tích khí chứa trong mỗi lốp xe là 120 lít và áp suất trong các lốp xe là 240 kPa. Coi gần đúng nhiệt độ của không khí trong lốp xe bằng với nhiệt độ ngoài trời. Hằng số Boltzmann \(k = {1,38.10^{ - 23}}{\rm{\;J}}/{\rm{K}}\).
a) Khi xe chạy liên tục trong thời gian dài dưới trời nắng nóng có thể dẫn đến nguy cơ nổ lốp xe, gây ra tai nạn.
b) Đến giữa trưa xe chạy đến Cam Lộ nhiệt độ trên mặt đường do được khoảng \({45^ \circ }{\rm{C}}\). Biết rằng khí trong lốp không thoát ra ngoài và thể tích lốp không thay đổi. Độ thay đổi động năng tịnh tiến trung bình của một phân tử do sự gia tăng nhiệt độ này bằng \({3,726.10^{ - 22}}J\).
c) Thực tế khi sử dụng nhiệt kế hồng ngoại đo nhiệt độ của lốp, người ta thấy nhiệt độ của lốp xe có thể đạt đến giá trị \({65^ \circ }{\rm{C}}\). Coi nhiệt độ khí trong lốp bằng nhiệt độ của lốp xe. Áp suất của khí trong lốp xe lúc này bằng \(557,8\,\,{\rm{kPa}}\).
d) Số mol khí trong mỗi lốp xe bằng \(11,55\,\,{\rm{mol}}\).
Một chiếc xe bán tải chạy trên đường cao tốc Bắc - Nam hướng đi từ Hà Nội đến Thành phố Hồ Chí Minh trong một ngày mùa hè. Xe đi vào sáng sớm với nhiệt độ ngoài trời là \({27^ \circ }{\rm{C}}\). Thể tích khí chứa trong mỗi lốp xe là 120 lít và áp suất trong các lốp xe là 240 kPa. Coi gần đúng nhiệt độ của không khí trong lốp xe bằng với nhiệt độ ngoài trời. Hằng số Boltzmann \(k = {1,38.10^{ - 23}}{\rm{\;J}}/{\rm{K}}\).
a) Khi xe chạy liên tục trong thời gian dài dưới trời nắng nóng có thể dẫn đến nguy cơ nổ lốp xe, gây ra tai nạn.
b) Đến giữa trưa xe chạy đến Cam Lộ nhiệt độ trên mặt đường do được khoảng \({45^ \circ }{\rm{C}}\). Biết rằng khí trong lốp không thoát ra ngoài và thể tích lốp không thay đổi. Độ thay đổi động năng tịnh tiến trung bình của một phân tử do sự gia tăng nhiệt độ này bằng \({3,726.10^{ - 22}}J\).
c) Thực tế khi sử dụng nhiệt kế hồng ngoại đo nhiệt độ của lốp, người ta thấy nhiệt độ của lốp xe có thể đạt đến giá trị \({65^ \circ }{\rm{C}}\). Coi nhiệt độ khí trong lốp bằng nhiệt độ của lốp xe. Áp suất của khí trong lốp xe lúc này bằng \(557,8\,\,{\rm{kPa}}\).
d) Số mol khí trong mỗi lốp xe bằng \(11,55\,\,{\rm{mol}}\).
Quảng cáo
Trả lời:
Phương pháp:
- Áp dụng các phương trình Clapeyron: \(pV = nRT\).
- Động năng tịnh tiến trung bình của phân tử khí: \({{\rm{W}}_d} = \frac{3}{2}kT\)
Cách giải:
a) Khi xe chạy liên tục trong thời gian dài dưới trời nắng nóng thì nhiệt độ của khí trong lốp xe tăng, áp suất tăng dẫn đến nguy cơ nổ lốp xe, gây tai nạn.
\( \to \) a đúng.
b) Độ thay đổi động năng tịnh tiến trung bình của một phần tử do sự gia tăng nhiệt độ là:
\({\rm{\Delta }}{{\rm{W}}_d} = \frac{3}{2}k\left( {{T_2} - {T_1}} \right)\)
\( \Rightarrow {\rm{\Delta }}{{\rm{W}}_d} = \frac{3}{2}{.1,38.10^{ - 23}}.\left( {45 - 27} \right) = {3,726.10^{ - 22}}\left( {\rm{J}} \right)\)
\( \to \) b đúng.
c) Vì thể tích khí không đổi nên ta có:
\(\frac{p}{T} = \) const \( \Rightarrow \frac{{240}}{{27 + 273}} = \frac{{{p_c}}}{{65 + 273}} \Rightarrow {p_c} = 270,4\left( {{\rm{kPa}}} \right)\)
\( \to \) c sai.
d) Áp dụng phương trình Clapeyron: \(pV = nRT\)
\( \Rightarrow {240.10^3}{.120.10^{ - 3}} = n.8,31.\left( {27 + 273} \right)\)
\( \Rightarrow n \approx 11,55\left( {{\rm{mol}}} \right)\)
\( \to \) d đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sổ tay Vật lí 12 (chương trình mới) ( 18.000₫ )
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp:
Áp dụng phương trình Clapeyron: \(pV = nRT = \frac{m}{M}RT\)
Cách giải:
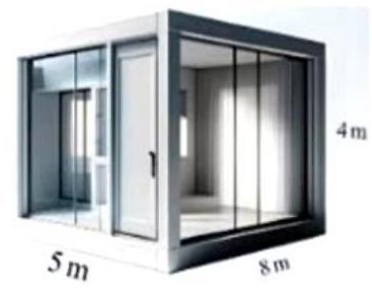
Phương trình Clapeyron: \(pV = \frac{m}{M}RT \Rightarrow pV = \frac{{{\rm{\Delta }}m}}{M}.R.{\rm{\Delta }}T\)
Thay số vào ta được:
\( \Rightarrow {1,013.10^5}.4.5.8 = \frac{{{\rm{\Delta }}m}}{{29}}.8,31.\left( {20 - 0} \right)\)
\( \Rightarrow {\rm{\Delta }}m \approx {2828.10^3}\left( {\rm{g}} \right) = 2828\left( {{\rm{kg}}} \right)\)
Lời giải
Phương pháp:
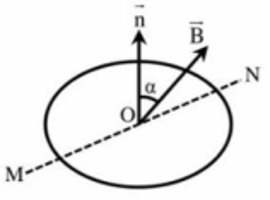
- Công thức tính từ thông: \({\rm{\Phi }} = NBS{\rm{cos}}\alpha \).
- Suất điện động cảm ứng có độ lớn: \({e_c} = N\left| {\frac{{{\rm{\Delta \Phi }}}}{{{\rm{\Delta }}t}}} \right| = N\left| {\frac{{{\rm{\Delta }}B.S.{\rm{cos}}\alpha }}{{{\rm{\Delta }}t}}} \right|\)
Cách giải:
a) Ta có: \(\left( {\vec B,mp} \right) = {60^ \circ } \Rightarrow \left( {\vec B,\vec n} \right) = 90 - 60 = {30^ \circ }\)
\( \to \) a sai.
b) Từ thông gửi qua khung dây:
\({\rm{\Phi }} = NBS.\cos \alpha = {10.0,4.15.10^{ - 4}}.{\rm{cos}}30\)
\( \Rightarrow {\rm{\Phi }} \approx {5,196.10^{ - 3}}\left( {{\rm{Wb}}} \right)\)
\( \to \) b sai.
c) Khi khung dây quay quanh đường kính MN một góc \({360^ \circ }\) thì khung dây quay trở về vị trí ban đầu \( \Rightarrow {\rm{\Delta \Phi }} = 0\)
\( \to \)c sai.
d) Suất điện động cảm ứng xuất hiện trong khung dây:
\({e_c} = N\left| {\frac{{{\rm{\Delta \Phi }}}}{{{\rm{\Delta }}t}}} \right| = N\left| {\frac{{{\rm{\Delta }}B.S.{\rm{cos}}\alpha }}{{{\rm{\Delta }}t}}} \right|\)
\( \Rightarrow {e_c} = 10.\left| {\frac{{\left( {0,1 - 0,04} \right){{.15.10}^{ - 4}}.{\rm{cos}}30}}{{0,05}}} \right| \approx 0,0156\left( {\rm{V}} \right)\)
Cường độ dòng điện cảm ứng xuất hiện trong khung có độ lớn:
\(i = \frac{{{e_c}}}{R} = \frac{{0,0156}}{{0,2}} = 0,78\left( A \right)\)
Câu 3
A. Giữa các phân tử có lực hút và lực đẩy gọi chung là lực liên kết phân tử.
B. Lực liên kết phân tử chỉ có lực hút, không có lực đẩy.
C. Các phân tử chuyển động không ngừng. Nhiệt độ của vật càng cao thì tốc độ chuyển động của các phân từ cấu tạo nên vật càng lớn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. bằng không.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\phi = BS{\rm{cos}}\alpha \)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.