Để xác định lượng máu trong bệnh nhân, người ta tiêm vào máu một người một lượng nhỏ dung dịch chứa đồng vị phóng xạ của \(\;_{11}^{124}{\rm{Na}}\) (chu kỳ bán rã 15 giờ) có độ phóng xạ \(2,5\mu {\rm{Ci}}\). Sau 7,5 giờ người ta lấy ra \(1{\rm{\;c}}{{\rm{m}}^3}\) máu người đó thì thấy nó có độ phóng xạ 508 phân rã/phút. Thể tích máu của người đó bằng bao nhiêu lít (Kết quả làm tròn đến 2 chữ số sau dấu phẩy thập phân).
Để xác định lượng máu trong bệnh nhân, người ta tiêm vào máu một người một lượng nhỏ dung dịch chứa đồng vị phóng xạ của \(\;_{11}^{124}{\rm{Na}}\) (chu kỳ bán rã 15 giờ) có độ phóng xạ \(2,5\mu {\rm{Ci}}\). Sau 7,5 giờ người ta lấy ra \(1{\rm{\;c}}{{\rm{m}}^3}\) máu người đó thì thấy nó có độ phóng xạ 508 phân rã/phút. Thể tích máu của người đó bằng bao nhiêu lít (Kết quả làm tròn đến 2 chữ số sau dấu phẩy thập phân).
Quảng cáo
Trả lời:
Phương pháp:
Công thức tính độ phóng xạ: \(H = {H_0}{.2^{ - \frac{t}{T}}}\)
Cách giải:
Gọi \(V\) là thể tích của máu trong người.
Ta có: \({H_0} = {2.10^{ - 6}}{.3,7.10^{10}} = 74000\left( {Bq} \right)\)
Sau 7,5h: \(H = \frac{{502}}{{60}}V \approx 8,37V\left( {Bq} \right)\)
Độ phóng xạ sau 7,5h là:
\(H = {H_0}{.2^{ - \frac{t}{T}}} = {H_0}{.2^{ - \frac{{7,5}}{{15}}}} \Rightarrow \frac{H}{{{H_0}}} = {2^{ - 2}}\)
\( \Rightarrow \frac{{8,37V}}{{74000}} = {2^{ - 2}} \Rightarrow V \approx 6251,6\left( {{\rm{c}}{{\rm{m}}^3}} \right) \approx 6,25\left( l \right)\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Sổ tay Vật lí 12 (chương trình mới) ( 18.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp:
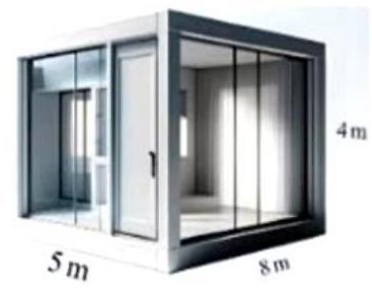
Áp dụng phương trình Clapeyron: \(pV = nRT = \frac{m}{M}RT\)
Cách giải:
Phương trình Clapeyron: \(pV = \frac{m}{M}RT \Rightarrow pV = \frac{{{\rm{\Delta }}m}}{M}.R.{\rm{\Delta }}T\)
Thay số vào ta được:
\( \Rightarrow {1,013.10^5}.4.5.8 = \frac{{{\rm{\Delta }}m}}{{29}}.8,31.\left( {20 - 0} \right)\)
\( \Rightarrow {\rm{\Delta }}m \approx {2828.10^3}\left( {\rm{g}} \right) = 2828\left( {{\rm{kg}}} \right)\)
Lời giải
Phương pháp:
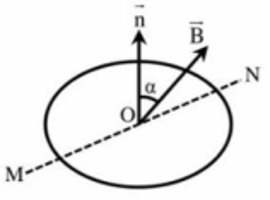
- Công thức tính từ thông: \({\rm{\Phi }} = NBS{\rm{cos}}\alpha \).
- Suất điện động cảm ứng có độ lớn: \({e_c} = N\left| {\frac{{{\rm{\Delta \Phi }}}}{{{\rm{\Delta }}t}}} \right| = N\left| {\frac{{{\rm{\Delta }}B.S.{\rm{cos}}\alpha }}{{{\rm{\Delta }}t}}} \right|\)
Cách giải:
a) Ta có: \(\left( {\vec B,mp} \right) = {60^ \circ } \Rightarrow \left( {\vec B,\vec n} \right) = 90 - 60 = {30^ \circ }\)
\( \to \) a sai.
b) Từ thông gửi qua khung dây:
\({\rm{\Phi }} = NBS.\cos \alpha = {10.0,4.15.10^{ - 4}}.{\rm{cos}}30\)
\( \Rightarrow {\rm{\Phi }} \approx {5,196.10^{ - 3}}\left( {{\rm{Wb}}} \right)\)
\( \to \) b sai.
c) Khi khung dây quay quanh đường kính MN một góc \({360^ \circ }\) thì khung dây quay trở về vị trí ban đầu \( \Rightarrow {\rm{\Delta \Phi }} = 0\)
\( \to \)c sai.
d) Suất điện động cảm ứng xuất hiện trong khung dây:
\({e_c} = N\left| {\frac{{{\rm{\Delta \Phi }}}}{{{\rm{\Delta }}t}}} \right| = N\left| {\frac{{{\rm{\Delta }}B.S.{\rm{cos}}\alpha }}{{{\rm{\Delta }}t}}} \right|\)
\( \Rightarrow {e_c} = 10.\left| {\frac{{\left( {0,1 - 0,04} \right){{.15.10}^{ - 4}}.{\rm{cos}}30}}{{0,05}}} \right| \approx 0,0156\left( {\rm{V}} \right)\)
Cường độ dòng điện cảm ứng xuất hiện trong khung có độ lớn:
\(i = \frac{{{e_c}}}{R} = \frac{{0,0156}}{{0,2}} = 0,78\left( A \right)\)
Câu 3
A. Giữa các phân tử có lực hút và lực đẩy gọi chung là lực liên kết phân tử.
B. Lực liên kết phân tử chỉ có lực hút, không có lực đẩy.
C. Các phân tử chuyển động không ngừng. Nhiệt độ của vật càng cao thì tốc độ chuyển động của các phân từ cấu tạo nên vật càng lớn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. bằng không.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(\phi = BS{\rm{cos}}\alpha \)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.