Một ống dây dẫn hình trụ dài gồm \({2.10^3}\) vòng dây, diện tích mỗi vòng dây là \(100{\rm{\;c}}{{\rm{m}}^2}\), điện trở \(16{\rm{\Omega }}\). Nối hai đầu ống dây bằng dây dẫn có điện trở không đáng kể. Đặt ống dây trong từ trường đều có vecto cảm ứng từ song song với trục của nó và có độ lớn tăng đề với tốc độ \({10^{ - 2}}{\rm{\;T}}/{\rm{s}}\). Công suất tỏa nhiệt của ống dây là:
Một ống dây dẫn hình trụ dài gồm \({2.10^3}\) vòng dây, diện tích mỗi vòng dây là \(100{\rm{\;c}}{{\rm{m}}^2}\), điện trở \(16{\rm{\Omega }}\). Nối hai đầu ống dây bằng dây dẫn có điện trở không đáng kể. Đặt ống dây trong từ trường đều có vecto cảm ứng từ song song với trục của nó và có độ lớn tăng đề với tốc độ \({10^{ - 2}}{\rm{\;T}}/{\rm{s}}\). Công suất tỏa nhiệt của ống dây là:
A. \({6,25.10^{ - 4}}{\rm{\;W}}\).
Quảng cáo
Trả lời:
Phương pháp:
Suất điện động cảm ứng trong ống dây: \(\left| {{e_c}} \right| = \left| {\frac{{{\rm{\Delta \Phi }}}}{{{\rm{\Delta }}t}}} \right| = N\left| {\frac{{{\rm{\Delta }}B}}{{{\rm{\Delta }}t}}} \right|S\)
Cường độ dòng điện cảm ứng trong ống dây dẫn: \({i_c} = \frac{{\left| {{e_c}} \right|}}{R}\)
Công suất nhiệt tỏa ra trong ống dây dẫn: \(P = R.i_c^2\)
Cách giải:
Từ thông qua ống dây dẫn gồm N vòng dây tính bằng \({\rm{\Phi }} = NBS\). Vì cảm ứng từ B tăng, nên từ thông \({\rm{\Phi }}\) tăng theo sao cho: \({\rm{\Delta \Phi }} = NS{\rm{\Delta }}B\)
Áp dụng công thức của định luật Faraday, ta xác định được độ lớn của suất điện động cảm ứng xuất hiện trong ống dây dẫn:
\(\left| {{e_c}} \right| = \left| {\frac{{{\rm{\Delta \Phi }}}}{{{\rm{\Delta }}t}}} \right| = N\left| {\frac{{{\rm{\Delta }}B}}{{{\rm{\Delta }}t}}} \right|S = {2.10^3}{.10^{ - 2}}{.100.10^{ - 4}} = 0,2\left( V \right)\)
Cường độ dòng điện cảm ứng chạy trong ống dây dẫn:
\({i_c} = \frac{{\left| {{e_c}} \right|}}{R} = \frac{{0,2}}{{16}} = 0,0125\left( A \right)\)
Áp dụng định luật Jun - Lenz, ta tính được công suất nhiệt toả ra trong ống dây dẫn:
\(P = R.i_c^2 = {16.0,0125^2} = {2,5.10^{ - 3}}\left( W \right)\)
Chọn B.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. tăng đồng thời áp suất khí tăng.
B. giảm đồng thời áp suất khí giảm.
Lời giải
Phương pháp:
Áp dụng định luật Boyle
Cách giải:
Theo định luật Boyle ta có: \({\rm{pV}} = \) hằng số
Ban đầu, pittong sát đầu trên của xilanh (thể tích của khí nhỏ)
Sau đó kéo pittong thì thể tích khí ở bên trong xilanh tăng lên
Suy ra: V tăng thì p giảm
Suy ra: Thể tích khí trong xilanh tăng đồng thời áp suất khí giảm.
Câu 2
Lời giải
Phương pháp:
Vận dụng kiến thức về thang đo:
+ Tạo phương trình tương ứng giữa hai thang đo nhiệt độ X và Y, dựa trên mối quan hệ tuyến tính giữa các thang đo.
+ Công thức tổng quát cho sự chuyển đổi giữa hai thang đo
Cách giải:
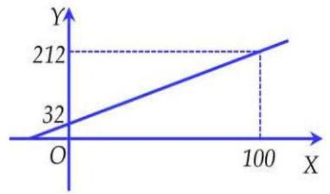
Ta có: \({T_Y} = a{T_X} + b\)
- Khi \({T_X} = 100X;{T_Y} = a.100 + b = 212Y\)
- Khi \({T_X} = 0X;{T_Y} = a.0 + b = 32Y\)
Giải hệ phương trình tìm được: \({\rm{a}} = 1,8;{\rm{b}} = 32\)
Thay các cặp giá trị đề bài đã cho vào biểu thức trên, ta xác định được: \({T_Y} = 1,8{T_X} + 32\)
Thay \({T_X} = 20X\) vào biểu thức vừa xác định, ta tính được: \({T_Y} = 68Y\)
Câu 3
A. b, d, e, c, a.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Nhôm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.