Một xilanh chứa \(0,3d{m^3}\) khí nitrogen ở nhiệt độ \({27^ \circ }{\rm{C}}\). Đun nóng đẳng áp khí đến \({127^ \circ }{\rm{C}}\). Thể tích khí nitrogen trong xilanh bây giờ bằng bao nhiêu \(d{m^3}\) (làm tròn kết quả đến chữ số hàng phần mười)?
Một xilanh chứa \(0,3d{m^3}\) khí nitrogen ở nhiệt độ \({27^ \circ }{\rm{C}}\). Đun nóng đẳng áp khí đến \({127^ \circ }{\rm{C}}\). Thể tích khí nitrogen trong xilanh bây giờ bằng bao nhiêu \(d{m^3}\) (làm tròn kết quả đến chữ số hàng phần mười)?
Quảng cáo
Trả lời:
Phương pháp:
Công thức định luật Charles: \(\frac{V}{T} = \) const
Cách giải:
Xét khối lượng khí không đổi.
Trạng thái 1: \(\left\{ {\begin{array}{*{20}{l}}{{V_1} = 0,3{\rm{d}}{{\rm{m}}^3}}\\{{T_1} = 27 + 273 = 300{\rm{\;K}}}\end{array}} \right.\)
Trạng thái \(2:\left\{ {\begin{array}{*{20}{l}}{{V_2}}\\{{T_1} = 127 + 273 = 400{\rm{\;K}}}\end{array}} \right.\)
Áp dụng công thức định luật Charles, ta có:
\(\frac{{{V_1}}}{{{T_1}}} = \frac{{{V_2}}}{{{T_2}}} \Rightarrow \frac{{0,3}}{{300}} = \frac{{{V_2}}}{{400}} \Rightarrow {V_2} = \frac{{0,3.400}}{{300}} = 0,4\left( {{\rm{d}}{{\rm{m}}^3}} \right)\)
Đáp số: 0,4
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. tăng đồng thời áp suất khí tăng.
B. giảm đồng thời áp suất khí giảm.
Lời giải
Phương pháp:
Áp dụng định luật Boyle
Cách giải:
Theo định luật Boyle ta có: \({\rm{pV}} = \) hằng số
Ban đầu, pittong sát đầu trên của xilanh (thể tích của khí nhỏ)
Sau đó kéo pittong thì thể tích khí ở bên trong xilanh tăng lên
Suy ra: V tăng thì p giảm
Suy ra: Thể tích khí trong xilanh tăng đồng thời áp suất khí giảm.
Câu 2
Lời giải
Phương pháp:
Vận dụng kiến thức về thang đo:
+ Tạo phương trình tương ứng giữa hai thang đo nhiệt độ X và Y, dựa trên mối quan hệ tuyến tính giữa các thang đo.
+ Công thức tổng quát cho sự chuyển đổi giữa hai thang đo
Cách giải:
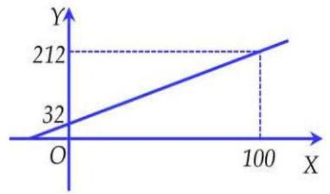
Ta có: \({T_Y} = a{T_X} + b\)
- Khi \({T_X} = 100X;{T_Y} = a.100 + b = 212Y\)
- Khi \({T_X} = 0X;{T_Y} = a.0 + b = 32Y\)
Giải hệ phương trình tìm được: \({\rm{a}} = 1,8;{\rm{b}} = 32\)
Thay các cặp giá trị đề bài đã cho vào biểu thức trên, ta xác định được: \({T_Y} = 1,8{T_X} + 32\)
Thay \({T_X} = 20X\) vào biểu thức vừa xác định, ta tính được: \({T_Y} = 68Y\)
Câu 3
A. b, d, e, c, a.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Nhôm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.