Một nhóm học sinh lớp 12 trường THPT Yên Thành 2 làm thí nghiệm để xác định nhiệt dung riêng của một mẫu kim loại. Họ có một bình xốp hình trụ có vỏ và nắp cách nhiệt, một que khuấy, một nhiệt kế, mẫu kim loại, một chiếc cân và một bình đun nước. Ban đầu, mẫu kim loại được để ở nhiệt độ \({27,0^ \circ }{\rm{C}}\).
a) Nhóm học sinh sử dụng cân và xác định được khối lượng nước đổ vào bình xốp là \(0,225{\rm{\;kg}}\), khối lượng của mẫu kim loại là \(0,409{\rm{\;kg}}\). Số chỉ của nhiệt kế nhúng trong nước nóng ngay trước khi thả mẫu kim loại là \({67,5^ \circ }{\rm{C}}\) và số chỉ của nhiệt kế khi mẩu kim loại và nước đạt trạng thái cân bằng nhiệt là \({56,0^ \circ }{\rm{C}}\). Biết nhiệt dung riêng của nước là \(4180{\rm{\;J/kg}}{\rm{.K}}\). Từ các số liệu trên, nhóm học sinh xác định được nhiệt dung riêng của mẫu kim loại xấp xỉ bằng \(912{\rm{\;J/kg}}{\rm{.K}}\).
b) Nhóm học sinh cho rằng, nếu đun nóng nước tới khoảng \({70,0^ \circ }{\rm{C}}\), đổ vào bình xốp đã cắm sẵn nhiệt kế, nhẹ nhàng nhúng chìm mẫu kim loại trong nước, đóng kín nắp lại và khuấy nhẹ tay thì số chỉ trên nhiệt kế sau đó sẽ thay đổi liên tục và chỉ dừng lại khi bình xốp chứa nước cùng mẫu kim loại đạt trạng thái cân bằng nhiệt.
c) Nhóm học sinh cho rằng, kết quả tính được ở câu a) nhỏ hơn giá trị nhiệt dung riêng chính xác của mẫu kim loại do trong phép tính đã bỏ qua nhiệt lượng trao đổi với môi trường.
d) Một học sinh trong nhóm cho rằng, nếu bỏ qua thất thoát nhiệt với môi trường thì nhiệt lượng nước thu vào bằng với nhiệt lượng mẫu kim loại tỏa ra.
Một nhóm học sinh lớp 12 trường THPT Yên Thành 2 làm thí nghiệm để xác định nhiệt dung riêng của một mẫu kim loại. Họ có một bình xốp hình trụ có vỏ và nắp cách nhiệt, một que khuấy, một nhiệt kế, mẫu kim loại, một chiếc cân và một bình đun nước. Ban đầu, mẫu kim loại được để ở nhiệt độ \({27,0^ \circ }{\rm{C}}\).
a) Nhóm học sinh sử dụng cân và xác định được khối lượng nước đổ vào bình xốp là \(0,225{\rm{\;kg}}\), khối lượng của mẫu kim loại là \(0,409{\rm{\;kg}}\). Số chỉ của nhiệt kế nhúng trong nước nóng ngay trước khi thả mẫu kim loại là \({67,5^ \circ }{\rm{C}}\) và số chỉ của nhiệt kế khi mẩu kim loại và nước đạt trạng thái cân bằng nhiệt là \({56,0^ \circ }{\rm{C}}\). Biết nhiệt dung riêng của nước là \(4180{\rm{\;J/kg}}{\rm{.K}}\). Từ các số liệu trên, nhóm học sinh xác định được nhiệt dung riêng của mẫu kim loại xấp xỉ bằng \(912{\rm{\;J/kg}}{\rm{.K}}\).
b) Nhóm học sinh cho rằng, nếu đun nóng nước tới khoảng \({70,0^ \circ }{\rm{C}}\), đổ vào bình xốp đã cắm sẵn nhiệt kế, nhẹ nhàng nhúng chìm mẫu kim loại trong nước, đóng kín nắp lại và khuấy nhẹ tay thì số chỉ trên nhiệt kế sau đó sẽ thay đổi liên tục và chỉ dừng lại khi bình xốp chứa nước cùng mẫu kim loại đạt trạng thái cân bằng nhiệt.
c) Nhóm học sinh cho rằng, kết quả tính được ở câu a) nhỏ hơn giá trị nhiệt dung riêng chính xác của mẫu kim loại do trong phép tính đã bỏ qua nhiệt lượng trao đổi với môi trường.
d) Một học sinh trong nhóm cho rằng, nếu bỏ qua thất thoát nhiệt với môi trường thì nhiệt lượng nước thu vào bằng với nhiệt lượng mẫu kim loại tỏa ra.
Quảng cáo
Trả lời:
Phương pháp:
+ Áp dụng phương trình cân bằng nhiệt để xác định nhiệt dung riêng.
+ Khi mẫu kim loại được nhúng vào nước nóng, nhiệt từ nước sẽ được truyền cho mẫu kim loại cho đến khi nhiệt độ của mẫu kim loại và nước đạt đến trạng thái cân bằng nhiệt.
+ Áp dụng phương trình cân bằng nhiệt để xác định nhiệt dung riêng khi không bỏ qua sự trao đổi nhiệt với môi trường.
Cách giải:
Áp dụng phương trình cân bằng nhiệt:
\({m_{kl}}.{c_{kl}}.\left( {{\rm{\Delta }}{t_{kl}}} \right) = {m_n}{c_n}{\rm{\Delta }}{t_n}\)
\( \Rightarrow 0,409.{c_{kl}}.\left( {56 - 27} \right) = 0,225.4180.\left( {67,5 - 56} \right)\)
\( \Rightarrow {c_{kl}} \approx 912\left( {{\rm{J/kg}}.{\rm{K}}} \right)\)
\( \to \) a đúng.
b) Khi mẫu kim loại được nhúng vào nước nóng, nhiệt từ nước sẽ được truyền cho mẫu kim loại cho đến khi nhiệt độ của mẫu kim loại và nước đạt đến trạng thái cân bằng nhiệt (cùng nhiệt độ). Sự thay đổi nhiệt độ sẽ liên tục cho đến khi cả nước và kim loại đạt nhiệt độ ổn định (trạng thái cân bằng nhiệt). Đây là nguyên lý cơ bản của thí nghiệm nhiệt học.
\( \to \) b đúng.
c) Nếu không bỏ qua sự trao đổi nhiệt với môi trường thì:
\(0,409.{c_{kl}}.\left( {56 - 27} \right) + {Q_{mt}} = 0,225.4180.\left( {67,5 - 56} \right)\)
\( \Rightarrow {c_{kl}} = \frac{{0,225.4180.\left( {67,5 - 56} \right) - {Q_{mt}}}}{{0,409.\left( {56 - 27} \right)}}\)
Vậy kết quả tính được ở câu a lớn hơn giá trị nhiệt dung riêng chính xác của mẫu kim loại.
\( \to \) c sai.
d) Nếu bỏ qua thất thoát nhiệt với môi trường thì nhiệt lượng mà nước tỏa ra bằng với nhiệt lượng mẫu kim loại thu vào.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Sổ tay Vật lí 12 (chương trình mới) ( 18.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp:
Áp dụng định luật Boyle cho hai trạng thái: Trước khi bơm và sau khi bơm.
Cách giải:
Trạng thái 1, xét tổng lượng khí sau 12 lần bơm và thể tích khí ban đầu trong quả bóng:
\(\left\{ {\begin{array}{*{20}{l}}{{p_1} = 1\left( {{\rm{atm}}} \right)}\\{{V_1} = 0,125.12 + 2,5 = 4\left( L \right)}\end{array}} \right.\)
Trạng thái 2, toàn bộ lượng khí trên được đưa vào bóng: \(\left\{ {\begin{array}{*{20}{l}}{{p_2}}\\{{V_2} = 2,5\left( L \right)}\end{array}} \right.\)
Vì nhiệt độ của khí không đổi nên áp dụng định luật Boyle:
\({p_1}{V_1} = {p_2}{V_2} \Rightarrow 1.4 = {p_2}.2,5\)
\( \Rightarrow {p_2} = 1,6\left( {{\rm{atm}}} \right)\)
Câu 2
Lời giải
Phương pháp:
Trong suốt quá trình chuyển thể nhiệt độ của chất đó không thay đổi.
Cách giải:
Từ bảng số liệu, nhiệt độ nóng chảy của tinh thể là \({72^ \circ }{\rm{C}}\).
Chọn C.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Giai đoạn từ (2) sang (3) là nén đẳng áp
B. Giai đoạn từ (1) sang (2) là dẫn đẳng nhiệt
C. Giai đoạn từ (1) sang (2) là nén đẳng áp
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. cả nhiệt độ và áp suất sẽ tiếp tục tăng.
B. áp suất sẽ tiếp tục tăng mặc dù nhiệt độ sôi không đổi.
C. khối lượng riêng của hơi nước sẽ giảm xuống.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
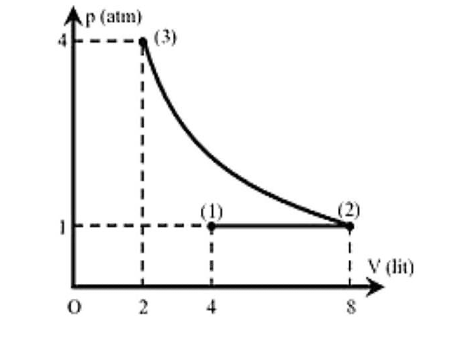 Chọn đáp án đúng:
Chọn đáp án đúng: