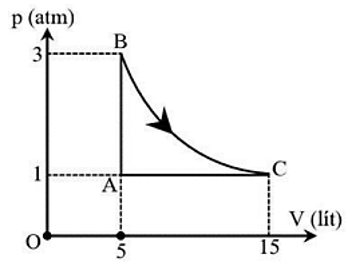
Một khối khí lý tưởng đơn nguyên tử có thể tích \({\rm{V}} = 5l\) ở áp suất khí quyển \(p = {1,013.10^5}{\rm{\;Pa}}\) và nhiệt độ \({\rm{T}} = 300{\rm{\;K}}\) (điểm A trong hình). Nó được làm nóng ở thể tích không đổi đến áp suất 3 atm (điểm B). Sau đó, nó được giãn nở đẳng nhiệt đến áp suất 1 atm (điểm C) và cuối cùng bị nén đẳng áp về trạng thái ban đầu.
a) Số mol của khí trong mẫu xấp xỉ là \(0,203{\rm{\;mol}}\).
b) Thể tích của khí ở C là 1,5 lít.
c) Nhiệt lượng khí nhận được trong quá trình \({\rm{A}} \to {\rm{B}}\) xấp xỉ là \(1,52{\rm{\;kJ}}\).
d) Trong quá trình \({\rm{B}} \to {\rm{C}}\) độ biến thiên động năng của khí \({\rm{\Delta }}U = 0\).
Một khối khí lý tưởng đơn nguyên tử có thể tích \({\rm{V}} = 5l\) ở áp suất khí quyển \(p = {1,013.10^5}{\rm{\;Pa}}\) và nhiệt độ \({\rm{T}} = 300{\rm{\;K}}\) (điểm A trong hình). Nó được làm nóng ở thể tích không đổi đến áp suất 3 atm (điểm B). Sau đó, nó được giãn nở đẳng nhiệt đến áp suất 1 atm (điểm C) và cuối cùng bị nén đẳng áp về trạng thái ban đầu.

a) Số mol của khí trong mẫu xấp xỉ là \(0,203{\rm{\;mol}}\).
b) Thể tích của khí ở C là 1,5 lít.
c) Nhiệt lượng khí nhận được trong quá trình \({\rm{A}} \to {\rm{B}}\) xấp xỉ là \(1,52{\rm{\;kJ}}\).
d) Trong quá trình \({\rm{B}} \to {\rm{C}}\) độ biến thiên động năng của khí \({\rm{\Delta }}U = 0\).
Quảng cáo
Trả lời:
Phương pháp:
Sử dụng lí thuyết về đồ thị của các đẳng quá trình
Phương trình Clapeyron: \({\rm{pV}} = {\rm{nRT}}\)
Phương trình trạng thái khí lí tưởng: \(\frac{{{p_1}{V_1}}}{{{T_1}}} = \frac{{{p_2}{V_2}}}{{{T_2}}}\)
Động năng của phân tử khí: \({W_d} = \frac{3}{2}kT\) với \(k = \frac{R}{{{N_A}}}\)
Nguyên lí I nhiệt động lực học: \({\rm{\Delta }}U = A + Q\)
Cách giải:
a) Áp dụng phương trình trạng thái khí lí tưởng, ta có:
\({1,013.10^5}{.5.10^{ - 3}} = n.8,31.300 \Rightarrow n = 0,203\left( {{\rm{mol}}} \right)\)
\( \to \) a đúng
b) Từ đồ thị, ta thấy thể tích ở C là 15 lít.
\( \to \) b sai
c) Đối với khí lí tưởng, nội năng U chỉ phụ thuộc vào động năng \({W_d}\) (mà động năng \({W_d}\) phụ thuộc vào nhiệt độ T)
Suy ra: \(U = \mathop \sum \nolimits^ {W_d}\)
Từ \({\rm{A}} \to {\rm{B}}\) là quá trình đẳng tích nên công \({\rm{A}} = 0\)
Độ biến thiên nội năng \({\rm{\Delta }}U = Q\)
Suy ra: \({\rm{\Delta }}U = {\rm{\Delta }}\mathop \sum \nolimits^ {W_d}\)
Động năng của phân tử khí: \({W_d} = \frac{3}{2}kT\) với \(k = \frac{R}{{{N_A}}}\)
\( \Rightarrow {\rm{\Delta }}U = Q = {\rm{\Delta }}\mathop \sum \nolimits^ {W_d} \Rightarrow {\rm{\Delta }}U = Q = n.{N_A}.\frac{3}{2}k.\left( {{T_B} - {T_A}} \right)\)
\( \Rightarrow {\rm{\Delta }}U = Q = n.{N_A}.\frac{3}{2}.\frac{R}{{{N_A}}}.\left( {{T_B} - {T_A}} \right)\)
\( \Rightarrow {\rm{\Delta }}U = Q = n.\frac{3}{2}.R.\left( {{T_B} - {T_A}} \right)\)
Có: \(\left\{ {\begin{array}{*{20}{l}}{{T_A} = 300K}\\{{p_B} = 3{p_A}}\\{{V_A} = {V_B}}\end{array}} \right.\)
\( \Rightarrow {T_B} = 3{T_A} = 3.300 = 900{\rm{\;K}}\)
\( \Rightarrow {\rm{\Delta }}U = Q = \frac{3}{2}.0,203 \cdot 8,31.\left( {900 - 300} \right) \approx 1518\left( {\rm{J}} \right) \approx 1,52\left( {{\rm{kJ}}} \right)\)
\( \to \) c đúng
d) Từ \({\rm{B}} \to {\rm{C}}\) là quá trình đẳng nhiệt
Mà độ biến thiên nội năng chỉ phụ thuộc vào nhiệt độ
Độ biến thiên nội năng của khí trong quá trình \({\rm{B}} \to {\rm{C}}\) là \({\rm{\Delta }}U = 0\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn Vật lí (Form 2025) ( 38.000₫ )
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Phương pháp:
Vận dụng quy tắc bàn tay phải
Độ lớn lực từ: \(F = BII{\rm{sin}}\alpha \)
Cách giải:
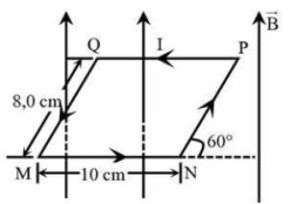
a) Lực từ tác dụng lên cạnh MN :
\({F_{MN}} = BIl{\rm{sin}}\alpha = 1,2.10.0,1.{\rm{sin}}{90^ \circ } = 1,2\left( N \right)\)
\( \to \) a sai
b) Áp dụng quy tắc bàn tay phải, lực từ tác dụng lên cạnh \(MQ\) của khung dây có chiều song song với \(\overrightarrow {NM} \).
\( \to \) b sai
c) Lực từ tác dụng lên hai cạnh MN và PQ của khung dây có độ lớn bằng nhau và ngược chiều nhau.
\( \to \) c đúng
d) Lực từ tác dụng lên cạnh NP:
\({F_{NP}} = BIl{\rm{sin}}\alpha = 1,2.10.0,08.{\rm{sin}}{30^ \circ } = 0,48\left( N \right)\)
Câu 2
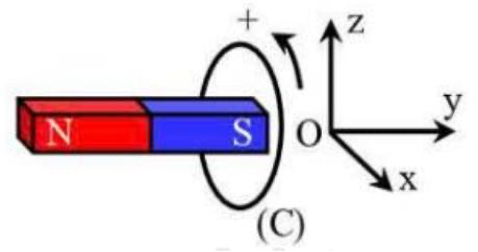
A. không có dòng điện cảm ứng.
B. có dòng điện cảm ứng chạy theo chiều dương.
C. có dòng điện cảm ứng chạy theo chiều âm.
Lời giải
Phương pháp:
Vận dụng kiến thức về dòng điện cảm ứng.
Cách giải:
Nếu cho \(\left( {\rm{C}} \right)\) quay đều theo chiều dương quanh trục quay song song với trục Oy thì trong \(\left( {\rm{C}} \right)\) không có dòng điện cảm ứng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.