Nhà máy đường kiểm tra khối lượng các gói đường do một máy đóng gói tự động thực hiện để kết luận máy vận hành tốt hay không. Kết quả kiểm tra được biểu diễn trong bảng dưới đây
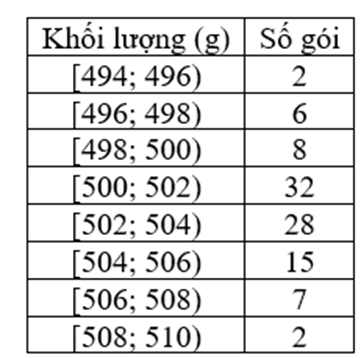
Biết rằng tiêu chuẩn mong muốn của nhà máy là khối lượng trung bình các gói đường nằm trong khoảng 500 – 504 gam và độ lệch chuẩn nhỏ hơn 3 gam thì xem như máy vận hành tốt.
(a) Tần số của nhóm [500; 502) bằng 32.
(b) Khối lượng trung bình của các gói đường của mẫu số liệu ghép nhóm trên là 502,22 gam.
(c) Độ lệch chuẩn của khối lượng các gói đường làm tròn đến hàng phần mười là 3,1.
(d) Sau khi kiểm tra nhà máy kết luận máy vận hành không tốt.
Quảng cáo
Trả lời:
Giải bởi Vietjack
a)Tần số của nhóm [500; 502) bằng 32.
b)
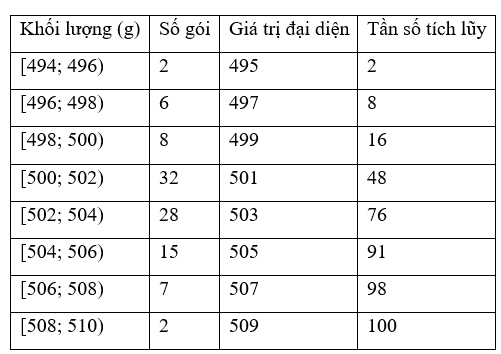
Ta có \(\overline x = \frac{{2.495 + 6.497 + 8.499 + 32.501 + 28.503 + 15.505 + 7.507 + 2.509}}{{100}} = 502,22\).
c) Phương sai
\[{s^2} = \frac{1}{{100}}\left[ \begin{array}{l}2.{\left( {495 - 502,22} \right)^2} + 6.{\left( {497 - 502,22} \right)^2} + 8.{\left( {499 - 502,22} \right)^2} + 32.{\left( {501 - 502,22} \right)^2}\\ + 28.{\left( {503 - 502,22} \right)^2} + 15.{\left( {505 - 502,22} \right)^2} + 7.{\left( {507 - 502,22} \right)^2} + 2.{\left( {509 - 502,22} \right)^2}\end{array} \right] = 7,8316\]
Độ lệch chuẩn \(s = \sqrt {7,8316} \approx 2,8\).
d) Vì \(\overline x = 502,22\) và s = 2,8 < 3 nên máy vận hàng tốt.
Đáp án: a) Đúng; b) Đúng; c) Sai; d) Sai.
Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay
Sách thầy cô Vietjack biên soạn:
- 250+ Công thức giải nhanh môn Toán 12 (chương trình mới) ( 18.000₫ )
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Số lượng khách du lịch đến tỉnh Quảng Ninh được cho dưới bảng sau
Cỡ mẫu n = 3 + 9 + 3 + 2 = 17.
Có \(\frac{n}{4} = 4,25\). Nhóm [5; 9) là nhóm đầu tiên có tần số tích lũy lớn hơn 4,25 nên nhóm này chứa tứ phân vị thứ nhất.
Ta có \({Q_1} = 5 + \frac{{\frac{{17}}{4} - 3}}{9}.4 = \frac{{50}}{9}\).
Có \(\frac{{3n}}{4} = 12,75\). Nhóm [9; 13) là nhóm đầu tiên có tần số tích lũy lớn hơn 12,75 nên nhóm này chứa tứ phân vị thứ ba.
Ta có \({Q_3} = 9 + \frac{{\frac{{3.17}}{4} - 12}}{3}.4 = 10\).
Khoảng tứ phân vị là Q = 10 – \(\frac{{50}}{9}\) ≈ 4,44.
Trả lời: 4,44.
Lời giải
Cỡ mẫu n = 50.
Có \(\frac{n}{4} = \frac{{50}}{4} = 12,5\). Nhóm [8; 10) là nhóm đầu tiên có tần số tích lũy lớn hơn 12,5 nên nhóm này chứa tứ phân vị thứ nhất.
Ta có \({Q_1} = 8 + \frac{{12,5 - 6}}{{14}}.2 \approx 8,93\).
Trả lời: 8,93.
Câu 3
A.
18,04.
B.
6,4.
C.
8,72.
D.
2,53.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A.
Khoảng biến thiên của mẫu số liệu là \[R = 20\].
B.
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là \[{Q_3} = 37\].
C.
Số trung bình của mẫu số liệu ghép nhóm là \[\overline x \approx 31,61\].
D.
Phương sai của mẫu số liệu ghép nhóm là \[{s^2} \approx 39,38\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A.
3,93.
B.
3,92.
C.
2,93.
D.
2,92.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A.
[20; 40).
B.
[0; 20).
C.
[40; 60).
D.
[60; 80).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo