Thống kê lượng khách du lịch đến tỉnh Quảng Ninh từ năm 2007 đến năm 2023 cho kết quả như sau (đơn vị: triệu người).
Ghép nhóm dãy số liệu trên thành các nhóm có độ dài bằng nhau đầu tiên là [1; 5) rồi cho biết khoảng tứ phân vị của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần trăm).
Quảng cáo
Trả lời:
Giải bởi Vietjack
Số lượng khách du lịch đến tỉnh Quảng Ninh được cho dưới bảng sau
Cỡ mẫu n = 3 + 9 + 3 + 2 = 17.
Có \(\frac{n}{4} = 4,25\). Nhóm [5; 9) là nhóm đầu tiên có tần số tích lũy lớn hơn 4,25 nên nhóm này chứa tứ phân vị thứ nhất.
Ta có \({Q_1} = 5 + \frac{{\frac{{17}}{4} - 3}}{9}.4 = \frac{{50}}{9}\).
Có \(\frac{{3n}}{4} = 12,75\). Nhóm [9; 13) là nhóm đầu tiên có tần số tích lũy lớn hơn 12,75 nên nhóm này chứa tứ phân vị thứ ba.
Ta có \({Q_3} = 9 + \frac{{\frac{{3.17}}{4} - 12}}{3}.4 = 10\).
Khoảng tứ phân vị là Q = 10 – \(\frac{{50}}{9}\) ≈ 4,44.
Trả lời: 4,44.
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
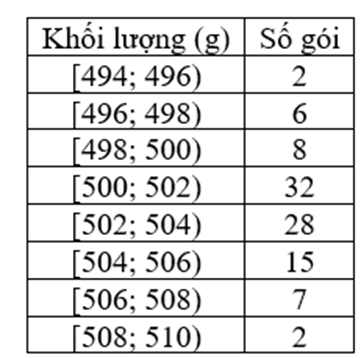
Cỡ mẫu n = 50.
Có \(\frac{n}{4} = \frac{{50}}{4} = 12,5\). Nhóm [8; 10) là nhóm đầu tiên có tần số tích lũy lớn hơn 12,5 nên nhóm này chứa tứ phân vị thứ nhất.
Ta có \({Q_1} = 8 + \frac{{12,5 - 6}}{{14}}.2 \approx 8,93\).
Trả lời: 8,93.
Câu 2
13,76.
13,88.
13,28.
13,75.
Lời giải
Đáp án đúngL C
Ta có \(\overline x = \frac{{11,5.4 + 12,5.12 + 13,5.16 + 14,5.5 + 15,5.3}}{{4 + 12 + 16 + 5 + 3}} = \frac{{531}}{{40}} \approx 13,28\).
Câu 3
Khoảng biến thiên của mẫu số liệu là \[R = 20\].
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là \[{Q_3} = 37\].
Số trung bình của mẫu số liệu ghép nhóm là \[\overline x \approx 31,61\].
Phương sai của mẫu số liệu ghép nhóm là \[{s^2} \approx 39,38\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
18,04.
6,4.
8,72.
2,53.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập