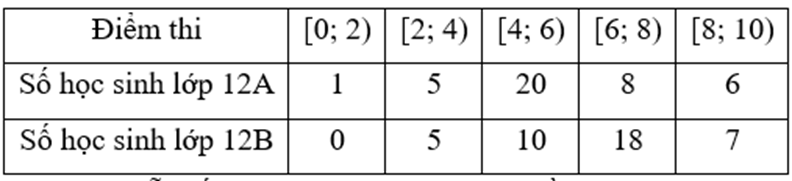
Mức thưởng tết (triệu đồng) cho các nhân viên của một công ty được thống kê trong bảng sau:
Khoảng biến thiên của mẫu số liệu ghép nhóm này là
A.
20.
B.
25.
C.
47.
D.
23.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng: B
R = 30 – 5 = 25.
Hot: Danh sách các trường đã công bố điểm chuẩn Đại học 2025 (mới nhất) (2025). Xem ngay
Sách thầy cô Vietjack biên soạn:
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 Bộ đề, Tổng ôn, sổ tay môn Toán (có đáp án chi tiết) ( 55.000₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Khoảng biến thiên của mẫu số liệu ghép nhóm trên là R = 10 – 5 = 5.
b) Xét mẫu số liệu khu vực A:
Cỡ mẫu n = 4 + 5 + 5 + 4 + 2 = 20.
Gọi x1; x2; …; x20 là mức lương khởi điểm của 20 công nhân được sắp theo thứ tự không giảm.
Ta có \({Q_1} = \frac{{{x_5} + {x_6}}}{2}\) mà x5; x6 [6; 7) nên nhóm này chứa tứ phân vị thứ nhất.
Ta có \({Q_1} = 6 + \frac{{\frac{{20}}{4} - 4}}{5}.1 = 6,2\).
Ta có \({Q_3} = \frac{{{x_{15}} + {x_{16}}}}{2}\) mà x15; x16 [8; 9) nên nhóm này chứa tứ phân vị thứ ba.
Ta có \({Q_3} = 8 + \frac{{\frac{{3.20}}{4} - 14}}{4}.1 = \frac{{33}}{4}\).
Suy ra \({\Delta _Q} = \frac{{33}}{4} - 6,2 \approx 2,1\).
c) Xét mẫu số liệu khu vực B.
Có cỡ mẫu n = 3 + 6 + 5 + 5 + 1 = 20.
Gọi y1; y2; …; y20 lần lượt là mức lương khởi điểm của công nhân khu vực B được sắp theo thứ tự không giảm.
Ta có \({Q_1} = \frac{{{y_5} + {y_6}}}{2}\) mà y5; y6 [6; 7) nên nhóm này chứa tứ phân vị thứ nhất.
Ta có \({Q_1} = 6 + \frac{{\frac{{20}}{4} - 3}}{6}.1 = \frac{{19}}{3}\).
Ta có \({Q_3} = \frac{{{y_{15}} + {y_{16}}}}{2}\) mà y15; y16 [8; 9) nên nhóm này chứa tứ phân vị thứ ba.
Ta có \({Q_3} = 8 + \frac{{\frac{{3.20}}{4} - 14}}{5}.1 = \frac{{41}}{5}\).
Suy ra \({\Delta _Q} = \frac{{41}}{5} - \frac{{19}}{3} \approx 1,9\).
d) Mức lương khởi điểm của khu vực B phân bố đồng đều hơn.
Đáp án: a) Đúng; b) Sai; c) Sai; d) Sai.
Câu 2
A.
15,25.
B.
20.
C.
4,75.
D.
5,2.
Lời giải
Đáp án đúng: C
Ta có n = 3 + 12 + 15 + 24 + 2 = 56.
Gọi x1; x2; ...; x56 lần lượt là thời gian truy cập internet mỗi buổi tối của 56 học sinh được sắp theo thứ tự không giảm.
Ta có \({Q_1} = \frac{{{x_{14}} + {x_{15}}}}{2}\) mà x14; x15 [12,5; 15,5) nên nhóm này chứa tứ phân vị thứ nhất.
Ta có \({Q_1} = 12,5 + \frac{{\frac{{56}}{4} - 3}}{{12}}.3 = 15,25\).
Ta có \({Q_3} = \frac{{{x_{42}} + {x_{43}}}}{2}\) mà \({x_{42}};{x_{43}} \in \left[ {18,5;21,5} \right)\)nên nhóm này chứa tứ phân vị thứ ba.
Ta có \({Q_3} = 18,5 + \frac{{\frac{{3.56}}{4} - 30}}{{24}}.3 = 20\).
Do đó \({\Delta _Q} = 20 - 15,25 = 4,75\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo