PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 18. Mỗi câu hỏi
thí sinh chỉ chọn một phương án.
Biết nhiệt nóng chảy riêng của nước đá ở là \(3,3 \cdot {10^5}\;{\rm{J}}/{\rm{kg}}\). Nhiệt lượng cần cung cấp để 30 g nước đá tan chảy hoàn toàn ở bằng
Quảng cáo
Trả lời:
\(Q = m\lambda = 0,03 \cdot 3,3 \cdot {10^5} = 9,9 \cdot {10^3}\;{\rm{J}}.{\rm{ }}\) Chọn B
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
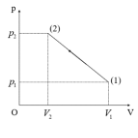
\(p = aV + b \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{p_1} = a{V_1} + b}\\{{p_2} = a{V_2} + b}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{5 = a.30 + b}\\{15 = a.10 + b}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = - 0,5}\\{b = 20}\end{array} \to p = - 0,5V + 20} \right.} \right.} \right.\)
\(\frac{{pV}}{T} = {\rm{ const }} \Rightarrow {T_{\max }}{\rm{ khi }}{(pV)_{\max }}\)
\(pV = - 0,5{V^2} + 20V\) đạo hàm được \( - V + 20 = 0 \Rightarrow V = 20{\rm{ lít}} \Rightarrow {(pV)_{\max }} = 200\)
\(\frac{{{W_{d\max }}}}{{{W_{d\min }}}} = \frac{{{T_{\max }}}}{{{T_{\min }}}} = \frac{{{{(pV)}_{\max }}}}{{{{(pV)}_{\min }}}} = \frac{{200}}{{150}} = \frac{4}{3} \approx 1,3\)
Trả lời ngắn: 1,3
Lời giải
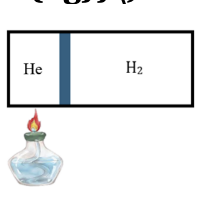
Khi pit-tông dịch chuyển đến chính giữa của xilanh thì p và V ở 2 phần bằng nhau
Trả lời ngắn: 327
Câu 3
A. còn 100 g nước đá.
B. còn 150 g nước đá
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.