thường được bợm khí hiếm nhẹ hơn không khí, nhờ đó có thể bay lên các tầng không khí khác nhau để thu thập thông tin về nhiệt độ, độ ẩm, áp suất, tốc độ gió. Người ta muốn chế tạo một bóng thám không có thể tăng bán kính lên tới 10 m khi bay ở tầng khí quyển có áp suất \(0,3 \cdot {10^5}\;{\rm{Pa}}\) và nhiệt độ 200 K. Biết bóng được bơm ở áp suất \(1,02 \cdot {10^5}\) Pa và nhiệt độ 300 K. Coi rằng quả bóng luôn có dạng hình cầu, bán kính của bóng khi vừa bơm xong bằng
Quảng cáo
Trả lời:
Chọn A
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
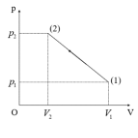
\(p = aV + b \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{p_1} = a{V_1} + b}\\{{p_2} = a{V_2} + b}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{5 = a.30 + b}\\{15 = a.10 + b}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = - 0,5}\\{b = 20}\end{array} \to p = - 0,5V + 20} \right.} \right.} \right.\)
\(\frac{{pV}}{T} = {\rm{ const }} \Rightarrow {T_{\max }}{\rm{ khi }}{(pV)_{\max }}\)
\(pV = - 0,5{V^2} + 20V\) đạo hàm được \( - V + 20 = 0 \Rightarrow V = 20{\rm{ lít}} \Rightarrow {(pV)_{\max }} = 200\)
\(\frac{{{W_{d\max }}}}{{{W_{d\min }}}} = \frac{{{T_{\max }}}}{{{T_{\min }}}} = \frac{{{{(pV)}_{\max }}}}{{{{(pV)}_{\min }}}} = \frac{{200}}{{150}} = \frac{4}{3} \approx 1,3\)
Trả lời ngắn: 1,3
Lời giải
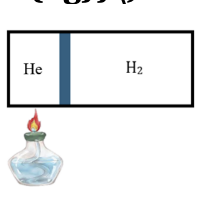
Khi pit-tông dịch chuyển đến chính giữa của xilanh thì p và V ở 2 phần bằng nhau
Trả lời ngắn: 327
Câu 3
A. còn 100 g nước đá.
B. còn 150 g nước đá
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.