Một học sinh tiến hành thí nghiệm khảo sát sự phụ thuộc của áp suất p theo nhiệt độ tuyệt đối \(T\) theo sơ đồ như hình bên. Trong đó, bình thủy tinh hình cầu có nút kín, bên trong có chứa 1 lít khí được nối thông với áp kế qua một ống nhỏ. Bình thủy tinh được nhúng trong một bình nước, nhiệt độ của nước được đo bởi một nhiệt kế. Coi rằng nhiệt độ khí trong bình luôn bằng nhiệt độ nước bên ngoài. Đun nóng từ từ nước trong bình rồi ghi lại giá trị nhiệt độ được chỉ bởi nhiệt kế và áp suất p được chi bởi áp kế thu được kết quả ở bảng bên.
Lần đo
\({\rm{p}}\left( {{{10}^5}\;{\rm{Pa}}} \right)\)
1
28,0
1,00
2
37,0
1,03
3
58,0
1,10
4
67,0
1,13
5
75,0
1,15
a) Quá trình biến đồi trạng thái khí trong bình là quá trình đẳng tích.
b) Động năng trung bình của các phân tử khí tại thời điểm lần đo thứ (3) lớn hơn gấp 2 lần động năng trung bình các phân tử khí tại thời điểm lần đo thứ (1).
c) Tỉ số \(\frac{{\rm{p}}}{{\rm{T}}}({\rm{Pa}}/{\rm{K}})\) có giá trị trung bình được làm tròn đến chữ số hàng đơn vị là 332.
d) Lượng khí đã dùng trong thí nghiệm được làm tròn đến chữ số hàng phần trăm là \(0,12\;{\rm{mol}}\).
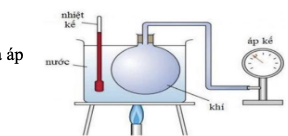
Một học sinh tiến hành thí nghiệm khảo sát sự phụ thuộc của áp suất p theo nhiệt độ tuyệt đối \(T\) theo sơ đồ như hình bên. Trong đó, bình thủy tinh hình cầu có nút kín, bên trong có chứa 1 lít khí được nối thông với áp kế qua một ống nhỏ. Bình thủy tinh được nhúng trong một bình nước, nhiệt độ của nước được đo bởi một nhiệt kế. Coi rằng nhiệt độ khí trong bình luôn bằng nhiệt độ nước bên ngoài. Đun nóng từ từ nước trong bình rồi ghi lại giá trị nhiệt độ được chỉ bởi nhiệt kế và áp suất p được chi bởi áp kế thu được kết quả ở bảng bên.
|
Lần đo |
\({\rm{p}}\left( {{{10}^5}\;{\rm{Pa}}} \right)\) |
|
|
1 |
28,0 |
1,00 |
|
2 |
37,0 |
1,03 |
|
3 |
58,0 |
1,10 |
|
4 |
67,0 |
1,13 |
|
5 |
75,0 |
1,15 |
a) Quá trình biến đồi trạng thái khí trong bình là quá trình đẳng tích.
b) Động năng trung bình của các phân tử khí tại thời điểm lần đo thứ (3) lớn hơn gấp 2 lần động năng trung bình các phân tử khí tại thời điểm lần đo thứ (1).
c) Tỉ số \(\frac{{\rm{p}}}{{\rm{T}}}({\rm{Pa}}/{\rm{K}})\) có giá trị trung bình được làm tròn đến chữ số hàng đơn vị là 332.
d) Lượng khí đã dùng trong thí nghiệm được làm tròn đến chữ số hàng phần trăm là \(0,12\;{\rm{mol}}\).

Quảng cáo
Trả lời:
Thể tích không đổi \( \Rightarrow \) a) Đúng
|
Lần đo |
\({\rm{T}}({\rm{K}})\) |
\(\frac{{\rm{p}}}{{\rm{T}}}\left( {\frac{{{\rm{Pa}}}}{{\rm{K}}}} \right)\) |
|
1 |
\(28 + 273 = 301\;{\rm{K}}\) |
\({10^5}/301\) |
|
2 |
\(37 + 273 = 310\;{\rm{K}}\) |
\({1,03.10^5}/310\) |
|
3 |
\(58 + 273 = 331\;{\rm{K}}\) |
\({1,1.10^5}/331\) |
|
4 |
\(67 + 273 = 340\;{\rm{K}}\) |
\({1,13.10^5}/340\) |
|
5 |
\(75 + 273 = 348\;{\rm{K}}\) |
\({1,15.10^5}/348\) |
\[{W_d}\~T \Rightarrow \frac{{{W_{d3}}}}{{{W_{d1}}}} = \frac{{{T_3}}}{{{T_1}}} = \frac{{331}}{{301}} \approx 1,1 \Rightarrow \] b) Sai
\(\frac{{\bar p}}{T} = \frac{{\frac{1}{{301}} + \frac{{1,03}}{{310}} + \frac{{1,1}}{{331}} + \frac{{1,13}}{{340}} + \frac{{1,15}}{{348}}}}{5} \cdot {10^5} \approx 332(\;{\rm{Pa}}/{\rm{K}}) \Rightarrow \)c) Đúng
\(\frac{{pV}}{T} = nR \Rightarrow 332 \cdot {10^{ - 3}} = n \cdot 8,31 \Rightarrow n \approx 0,04\;{\rm{mol}} \Rightarrow \)d) Sai
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
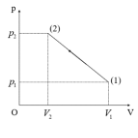
\(p = aV + b \Rightarrow \left\{ {\begin{array}{*{20}{l}}{{p_1} = a{V_1} + b}\\{{p_2} = a{V_2} + b}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{5 = a.30 + b}\\{15 = a.10 + b}\end{array} \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = - 0,5}\\{b = 20}\end{array} \to p = - 0,5V + 20} \right.} \right.} \right.\)
\(\frac{{pV}}{T} = {\rm{ const }} \Rightarrow {T_{\max }}{\rm{ khi }}{(pV)_{\max }}\)
\(pV = - 0,5{V^2} + 20V\) đạo hàm được \( - V + 20 = 0 \Rightarrow V = 20{\rm{ lít}} \Rightarrow {(pV)_{\max }} = 200\)
\(\frac{{{W_{d\max }}}}{{{W_{d\min }}}} = \frac{{{T_{\max }}}}{{{T_{\min }}}} = \frac{{{{(pV)}_{\max }}}}{{{{(pV)}_{\min }}}} = \frac{{200}}{{150}} = \frac{4}{3} \approx 1,3\)
Trả lời ngắn: 1,3
Lời giải
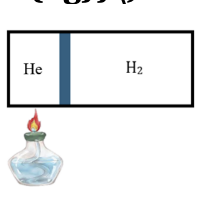
Khi pit-tông dịch chuyển đến chính giữa của xilanh thì p và V ở 2 phần bằng nhau
Trả lời ngắn: 327
Câu 3
A. còn 100 g nước đá.
B. còn 150 g nước đá
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.