Bác An có một khu vườn, bác chia khu vườn thành hai phần như hình vẽ:
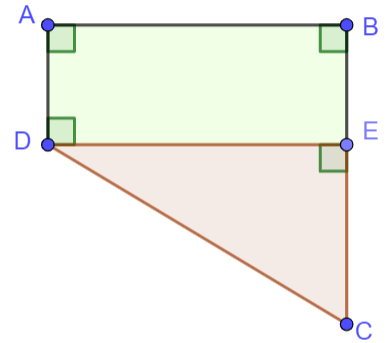
Phần màu nâu dùng để trồng rau có diện tích là \(30\;{{\rm{m}}^2}.\) Phần màu xanh dùng để trồng cây ăn quả.
Biết rằng \(AD = 4\;{\rm{m}},\;BC = 10\;{\rm{m}}.\) Hỏi độ dài \(AB\) bằng bao nhiêu mét?
Bác An có một khu vườn, bác chia khu vườn thành hai phần như hình vẽ:
Phần màu nâu dùng để trồng rau có diện tích là \(30\;{{\rm{m}}^2}.\) Phần màu xanh dùng để trồng cây ăn quả.
Biết rằng \(AD = 4\;{\rm{m}},\;BC = 10\;{\rm{m}}.\) Hỏi độ dài \(AB\) bằng bao nhiêu mét?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án: \(10\)
Tứ giác \(ABED\) có: \(\widehat A = \widehat B = \widehat {BED} = \widehat {EDA} = 90^\circ \) nên tứ giác \(ABED\) là hình chữ nhật.
Do đó, \(EB = AD = 4\;{\rm{m,}}\;AB = DE.\)
Ta có: \(EC = CB - BE = 10 - 4 = 6\;\left( {\rm{m}} \right).\)
Diện tích tam giác \(DEC\) vuông tại \(E\) bằng \(30\;{{\rm{m}}^2}\) nên
\(\frac{1}{2}EC \cdot DE = 30\) \(\)
\(\frac{1}{2} \cdot 6 \cdot DE = 30\)
\(DE = 10\;{\rm{m}}.\)
Do đó, \(AB = DE = 10\;{\rm{m}}.\) Vậy \(AB = 10\;{\rm{m}}.\)
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(AC = \frac{1}{2}BD.\)
B. \(AC = \frac{3}{4}BD.\)
C. \(AC = \frac{4}{3}BD.\)
D. \(AC = BD.\)
Lời giải
Đáp án đúng là: D
Hình bình hành \(ABCD\) có \(\widehat A = 90^\circ \) nên \(ABCD\) là hình chữ nhật. Do đó, \(AC = BD.\)
Câu 2
A. \(\widehat {OAB} = \widehat {OBA}.\)
B. \(\widehat {OAB} = 2\widehat {OBA}.\)
C. \(\widehat {OAB} = \frac{1}{2}\widehat {OBA}.\)
D. \(\widehat {OAB} = \frac{1}{3}\widehat {OBA}.\)
Lời giải
Đáp án đúng là: A
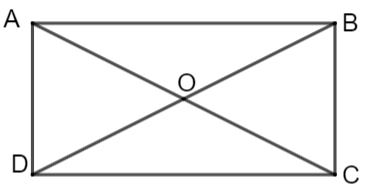
Vì tứ giác \(ABCD\) là hình chữ nhật nên \(OA = OB.\) Do đó, tam giác \(OAB\) cân tại \(O.\) Nên \(\widehat {OAB} = \widehat {OBA}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. \(AD = 4\;{\rm{cm}}{\rm{.}}\)
B. \(AD = 6\;{\rm{cm}}{\rm{.}}\)
C. \(AD = 5\;{\rm{cm}}{\rm{.}}\)
D. \(AD = 10\;{\rm{cm}}{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Hình thang có hai góc vuông là hình chữ nhật.
B. Hình thang có hai đường chéo bằng nhau là hình chữ nhật.
C. Hình thang cân có một góc vuông là hình chữ nhật.
D. Cả A, B, C đều đúng.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo