Cho tam giác \(ABC\) cân tại \(A\) có \(M,\;N\) lần lượt là trung điểm của \(AC,\;AB.\) Gọi \(G\) là giao điểm của \(BM\) và \(CN.\) Trên tia đối của \(GB,\;GC\) lần lượt lấy các điểm \(D,\;E\) sao cho \(GD = GB,\;GE = GC.\)
a) \(G\) là trọng tâm của tam giác \(ABC.\)
b) \(\Delta BMC = \Delta BCN.\)
c) \(BD = CE.\)
d) \(\widehat {EBC} = 90^\circ .\)
Cho tam giác \(ABC\) cân tại \(A\) có \(M,\;N\) lần lượt là trung điểm của \(AC,\;AB.\) Gọi \(G\) là giao điểm của \(BM\) và \(CN.\) Trên tia đối của \(GB,\;GC\) lần lượt lấy các điểm \(D,\;E\) sao cho \(GD = GB,\;GE = GC.\)
a) \(G\) là trọng tâm của tam giác \(ABC.\)
b) \(\Delta BMC = \Delta BCN.\)
c) \(BD = CE.\)
d) \(\widehat {EBC} = 90^\circ .\)
Câu hỏi trong đề: Trắc nghiệm Hình chữ nhật lớp 8 (có đáp án) !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
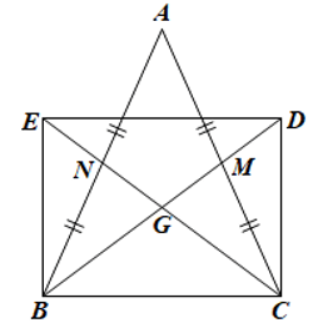
a) Đúng.
Vì \(G\) là giao điểm của hai đường trung tuyến \(BM,\;CN\) của \(\Delta ABC\) nên \(G\) là trọng tâm của \(\Delta ABC.\)
b) Sai.
Vì tam giác \(ABC\) cân tại \(A\) nên \(AB = AC,\;\widehat {ABC} = \widehat {ACB}.\)
Vì \(M\) là trung điểm của \(AC\) nên \(AM = MC = \frac{1}{2}AC.\)
Vì \(N\) là trung điểm của \(AB\) nên \(AN = NB = \frac{1}{2}AB.\)
Do đó, \(AN = NB = AM = MC.\)
Tam giác \(BMC\) và tam giác \(CNB\) có: \(\widehat {MCB} = \widehat {NBC}\;\left( {cmt} \right),\;MC = BN\;\left( {cmt} \right),\;BC\;{\rm{chung}}{\rm{.}}\)
Do đó, \(\Delta BMC = \Delta CNB\;\left( {c - g - c} \right).\)
c) Đúng.
Vì \(\Delta BMC = \Delta CNB\;\left( {cmt} \right)\) nên \(BM = CN.\)
Vì \(G\) là trọng tâm của \(\Delta ABC\) nên \(GC = \frac{2}{3}CN,\;BG = \frac{2}{3}BM.\) Suy ra: \(GB = GC.\)
Mà \(GD = GB,\;GE = GC\) nên \(GD = GB = GE = GC.\) Suy ra: \(EG + GC = BG + GD\) hay \(BD = CE.\)
d) Đúng.
Tứ giác \(BEDC\) có hai đường chéo \(CE,\;BD\) cắt nhau tại \(G;\;\) \(G\) vừa là trung điểm của \(BD\) vừa là trung điểm của \(EC.\) Do đó, tứ giác \(BEDC\) là hình bình hành. Mà \(BD = CE\) nên tứ giác \(BEDC\) là hình chữ nhật. Do đó, \(\widehat {EBC} = 90^\circ .\)
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Lời giải
Đáp án đúng là: D
Hình bình hành \(ABCD\) có \(\widehat A = 90^\circ \) nên \(ABCD\) là hình chữ nhật. Do đó, \(AC = BD.\)
Câu 2
Lời giải
Đáp án đúng là: A
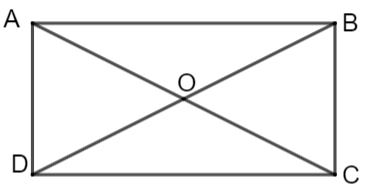
Vì tứ giác \(ABCD\) là hình chữ nhật nên \(OA = OB.\) Do đó, tam giác \(OAB\) cân tại \(O.\) Nên \(\widehat {OAB} = \widehat {OBA}.\)
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập