Tìm giá trị lớn nhất và nhỏ nhất (nếu có) của hàm số sau trên đoạn đã chỉ ra.
a) \(f\left( x \right) = \frac{{2x + 3}}{{x + 1}}\) trên đoạn \(\left[ {0;4} \right]\);
b) \(f\left( x \right) = \frac{{2{x^2} + 4x + 5}}{{{x^2} + 1}}\) trên \(\mathbb{R}\).
Tìm giá trị lớn nhất và nhỏ nhất (nếu có) của hàm số sau trên đoạn đã chỉ ra.
a) \(f\left( x \right) = \frac{{2x + 3}}{{x + 1}}\) trên đoạn \(\left[ {0;4} \right]\);
b) \(f\left( x \right) = \frac{{2{x^2} + 4x + 5}}{{{x^2} + 1}}\) trên \(\mathbb{R}\).
Quảng cáo
Trả lời:
a) Có \(f'\left( x \right) = - \frac{1}{{{{\left( {x + 1} \right)}^2}}} < 0,\forall x \in \left[ {0;4} \right]\). Suy ra hàm số đã cho nghịch biến trên đoạn \([0;4]\).
Vậy \(\mathop {\max }\limits_{\left[ {0;4} \right]} f\left( x \right) = f\left( 0 \right) = 3;\mathop {\min }\limits_{\left[ {0;4} \right]} f\left( x \right) = f\left( 4 \right) = \frac{{11}}{5}\).
b) Có \(f'\left( x \right) = \frac{{ - 4{x^2} - 6x + 4}}{{{{\left( {{x^2} + 1} \right)}^2}}}\); \(f'\left( x \right) = 0 \Leftrightarrow - 4{x^2} - 6x + 4 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = \frac{1}{2}\end{array} \right.\).
Bảng biến thiên
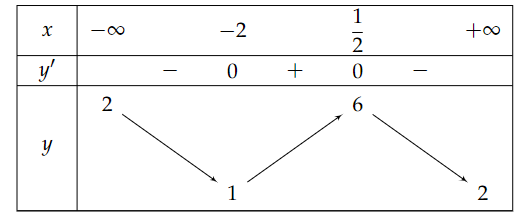
Dựa vào bảng biến thiên, ta có: \(\mathop {\min }\limits_\mathbb{R} f\left( x \right) = f\left( { - 2} \right) = 1;\mathop {\max }\limits_\mathbb{R} f\left( x \right) = f\left( {\frac{1}{2}} \right) = 6\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi x (triệu VNĐ) là số tiền cần giảm cho mỗi chiếc xe\[\left( {0 \le x \le 4} \right).\]
Số lượng xe bán ra được trong một năm sau khi giảm giá là: \[x.200 + 600\](chiếc)
Số lợi nhuận thu được từ việc bán xe trong một năm sau khi giảm giá là: \[\left( {x.200 + 600} \right)\left( {4 - x} \right)\]
Xét hàm số \[f\left( x \right) = \left( {x.200 + 600} \right)\left( {4 - x} \right) = 200\left( { - {x^2} + x + 12} \right)\,\,\,\left( {0 \le x \le 4} \right)\].
Có \(f'\left( x \right) = 200\left( { - 2x + 1} \right)\); \(f'\left( x \right) = 0 \Leftrightarrow - 2x + 1 = 0 \Leftrightarrow x = \frac{1}{2}\).
Có \(f\left( 0 \right) = 2400;f\left( {\frac{1}{2}} \right) = 2450;f\left( 4 \right) = 0\).
Lời giải
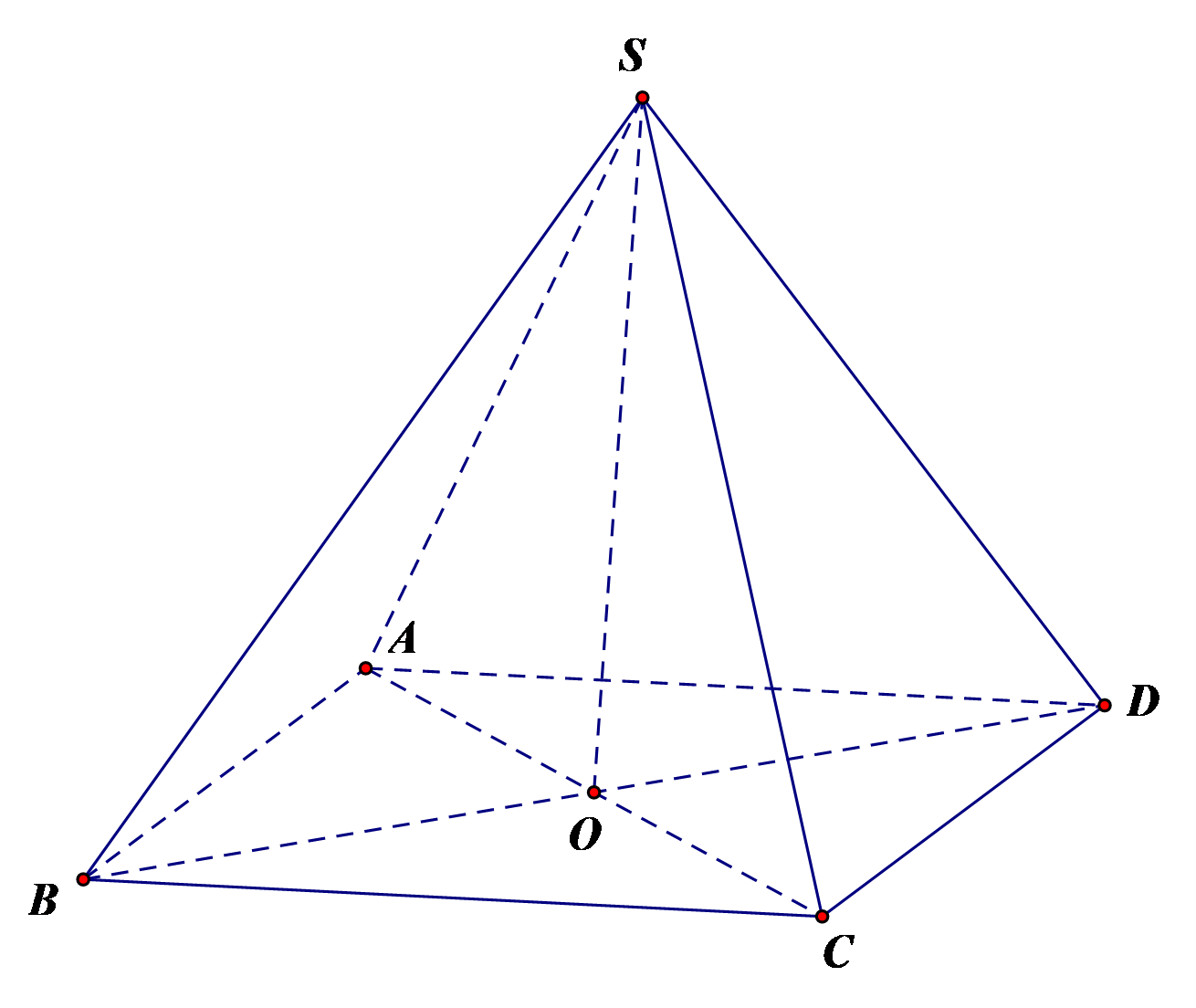
a) \(\overrightarrow {SA} ,\overrightarrow {SB} ,\overrightarrow {SC} ,\overrightarrow {SD} \) là 4 vectơ không đồng phẳng.
Vì 5 điểm S, A, B, C, D không cùng thuộc 1 mặt phẳng.
b) \(\left| {\overrightarrow {SA} } \right| = \left| {\overrightarrow {SB} } \right| = \left| {\overrightarrow {SC} } \right| = \left| {\overrightarrow {SD} } \right|\) .
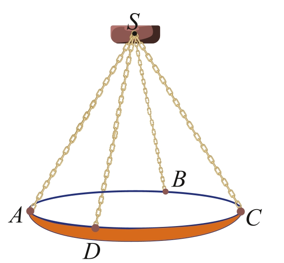
c) Độ lớn trọng lực tác động lên đèn chùm là: \(P = mg = 5.10 = 50\;N\).
d) Ta có \(S.ABCD\) là hình chóp tứ giác đều. Suy ra \(SA = SB = SC = SD\) mà \(\widehat {ASC} = 60^\circ \).
Vậy tam giác \[SAC\] đều. Gọi \[O\] là trung điểm \(AC\).
Hợp lực của 4 sợi xích là: \(\vec F = \overrightarrow {SA} + \overrightarrow {SC} + \overrightarrow {SB} + \overrightarrow {SD} = 2\overrightarrow {SO} + 2\overrightarrow {SO} = 4\overrightarrow {SO} \)
Để đèn chùm đứng yên thì hợp lực của các sợi xích phải cân bằng với trọng lực hay \(4\overrightarrow {SO} = \vec P\) hay \(4SO = P \Leftrightarrow SO = 12,5\).
Xét tam giác đều \(SAC\)có \(SA = \frac{2}{{\sqrt 3 }}SO = \frac{{25\sqrt 3 }}{3}\).
Vậy độ lớn của lực căng cho mỗi sợi xích là \(\frac{{25\sqrt 3 }}{3}\;N\).
Đáp án: a) Sai; b) Đúng; c) Đúng; d) Sai.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.