Một chiếc đồng hồ có kim giờ \(OM\) chỉ số 12, kim phút \(ON\) chỉ số 3.
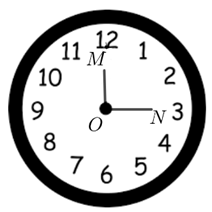
Số đo của góc lượng giác \(\left( {OM,ON} \right)\) là
A.
\[ - \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}\].
B.
\[ - \frac{{3\pi }}{2} + k2\pi ,k \in \mathbb{Z}\].
C.
\[\pi + k2\pi ,k \in \mathbb{Z}\].
D.
\[\frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}\].
Quảng cáo
Trả lời:
Giải bởi Vietjack
Khi kim giờ \(OM\) chỉ số 12, kim phút \(ON\) chỉ số 3 thì \(\widehat {MON} = \frac{\pi }{2}\).
Từ hình vẽ ta thấy góc lượng giác \(\left( {OM,ON} \right)\) có tia đầu \(OM,\) tia cuối \(ON\), quay theo chiều dương (ngược chiều quay của kim đồng hồ) nên \(\left( {OM,ON} \right) = 2\pi - \frac{\pi }{2} + k2\pi = \frac{{3\pi }}{2} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\) hoặc nếu theo chiều âm có thể kết luận \[\left( {OM,\,\,ON} \right) = - \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}\]. Chọn A.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Sử, Địa, GD KTPL 11 cho cả 3 bộ Kết nối, Chân trời, Cánh diều VietJack - Sách 2025 ( 38.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Ta có \(4\sin 3x\sin 2x\cos x = 4\left( {\sin 3x\cos x} \right)\sin 2x = 4 \cdot \frac{1}{2}\left( {\sin 4x + \sin 2x} \right)\sin 2x\)
\( = 2\sin 4x\sin 2x + 2{\sin ^2}2x = \left( {\cos 2x - \cos 6x} \right) + 2\left( {\frac{{1 - \cos 4x}}{2}} \right)\)\( = \cos 2x - \cos 4x - \cos 6x + 1\).
Vậy \(a + b + c + d = 0\).
Đáp án:0.
Lời giải
a) Nhiệt độ ngoài trời lúc 19 giờ là \(h\left( {19} \right) = 31 + 3\sin \frac{\pi }{{12}}\left( {19 - 9} \right)\)\( = 31 + 3\sin \frac{{5\pi }}{6} = 32,5\)℃.
b) Ta có \( - 1 \le \sin \frac{\pi }{{12}}\left( {t - 9} \right) \le 1 \Rightarrow - 3 \le 3\sin \frac{\pi }{{12}}\left( {t - 9} \right) \le 3 \Rightarrow 28 \le 31 + 3\sin \frac{\pi }{{12}}\left( {t - 9} \right) \le 34\,\,\forall t.\)
Do đó \(\max h\left( t \right) = 34 \Leftrightarrow \sin \frac{\pi }{{12}}\left( {t - 9} \right) = 1 \Leftrightarrow \frac{\pi }{{12}}\left( {t - 9} \right) = \frac{\pi }{2} + k2\pi \Leftrightarrow t = 15 + 24k,k \in \mathbb{Z}.\)
Vì \(0 < t \le 24 \Rightarrow 0 \le 15 + 24k \le 24 \Leftrightarrow - \frac{{15}}{{24}} \le k \le \frac{3}{8}\).
Do \(k \in \mathbb{Z} \Rightarrow k = 0\) nên \(t = 15.\)
Vậy vào thời điểm 15 giờ thì nhiệt độ ở thành phố đó lớn nhất.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A.
\(\left( {0;\pi } \right)\).
B.
\(\left( {\frac{{3\pi }}{2};\frac{{5\pi }}{2}} \right)\).
C.
\(\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right)\).
D.
\(\left( { - 3\pi ; - 2\pi } \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
![Cho mẫu số liệu ghép nhóm về chiều cao của \[25\]cây dừa giống, như sau:
Mốt của mẫu số liệu ghép nhóm này là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/blobid2-1757597535.png)
A.
\[{M_o} = \frac{{50}}{3}\].
B.
\[{M_o} = \frac{{70}}{3}\].
C.
\[{M_o} = \frac{{70}}{2}\].
D.
\[{M_o} = \frac{{80}}{3}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A.
\(d = - 2\).
B.
\(d = 1\).
C.
\(d = 3\).
D.
\(d = 2\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo