Bộ 5 đề thi giữa kì 1 Toán 11 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Đề 4
22 người thi tuần này 4.6 1.3 K lượt thi 21 câu hỏi 60 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 3
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 2
Đề kiểm tra Bài tập cuối chương 9 (có lời giải) - Đề 1
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 2
Đề kiểm tra Biến cố hợp biến cố giao và quy tắc cộng xác suất (có lời giải) - Đề 1
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 3
Đề kiểm tra Biến cố giao và quy tắc nhân xác suất (có lời giải) - Đề 2
Danh sách câu hỏi:
Câu 1
\[ - \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}\].
\[ - \frac{{3\pi }}{2} + k2\pi ,k \in \mathbb{Z}\].
\[\pi + k2\pi ,k \in \mathbb{Z}\].
\[\frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}\].
Lời giải
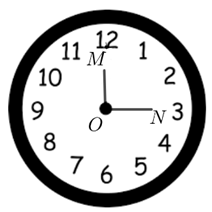
Khi kim giờ \(OM\) chỉ số 12, kim phút \(ON\) chỉ số 3 thì \(\widehat {MON} = \frac{\pi }{2}\).
Từ hình vẽ ta thấy góc lượng giác \(\left( {OM,ON} \right)\) có tia đầu \(OM,\) tia cuối \(ON\), quay theo chiều dương (ngược chiều quay của kim đồng hồ) nên \(\left( {OM,ON} \right) = 2\pi - \frac{\pi }{2} + k2\pi = \frac{{3\pi }}{2} + k2\pi \,\,\left( {k \in \mathbb{Z}} \right)\) hoặc nếu theo chiều âm có thể kết luận \[\left( {OM,\,\,ON} \right) = - \frac{\pi }{2} + k2\pi ,k \in \mathbb{Z}\]. Chọn A.
Câu 2
\( - \frac{1}{3}.\)
\(\frac{2}{3}.\)
\( - \frac{2}{3}.\)
\(\frac{1}{3}.\)
Lời giải
Ta có \(\sin \left( {\alpha - \frac{{3\pi }}{2}} \right) = \sin \alpha \cos \frac{{3\pi }}{2} - \cos \alpha \sin \frac{{3\pi }}{2} = \sin \alpha \cdot 0 - \frac{1}{3} \cdot \left( { - 1} \right) = \frac{1}{3}\). Chọn D.
Câu 3
\(\left( {0;\pi } \right)\).
\(\left( {\frac{{3\pi }}{2};\frac{{5\pi }}{2}} \right)\).
\(\left( { - \frac{{3\pi }}{2}; - \frac{\pi }{2}} \right)\).
\(\left( { - 3\pi ; - 2\pi } \right)\).
Lời giải
Ta thấy đồ thị hàm số \(y = \cos x\) đi lên từ trái sang phải khi \(x \in \left( { - 3\pi ; - 2\pi } \right)\). Do đó hàm số \(y = \cos x\) đồng biến trên khoảng \(\left( { - 3\pi ; - 2\pi } \right)\). Chọn D.
Câu 4
\(x = \frac{\pi }{4} + k\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{\pi }{4} + k2\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{\pi }{2} + k2\pi {\rm{ }}\left( {k \in \mathbb{Z}} \right)\).
\(x = \frac{{k\pi }}{2}{\rm{ }}\left( {k \in \mathbb{Z}} \right)\).
Lời giải
Ta có \(\sin 2x = 1 \Leftrightarrow 2x = \frac{\pi }{2} + k2\pi \Leftrightarrow x = \frac{\pi }{4} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\). Chọn A.
Câu 5
\({u_5} = \frac{{17}}{{12}}.\)
\({u_5} = \frac{{71}}{{39}}.\)
\({u_5} = \frac{7}{4}.\)
\({u_5} = \frac{1}{4}.\)
Lời giải
Ta có \({u_5} = \frac{{2 \cdot {5^2} - 1}}{{{5^2} + 3}} = \frac{7}{4}\). Chọn C.
Câu 6
\(d = - 2\).
\(d = 1\).
\(d = 3\).
\(d = 2\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
\({u_n} = \frac{1}{n}\).
\({u_n} = 3n\).
\({u_n} = {2^n} + 1\).
\({u_n} = {2^n}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
\(25\).
\(26\).
\(27\).
\(28\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
\[{M_o} = \frac{{50}}{3}\].
\[{M_o} = \frac{{70}}{3}\].
\[{M_o} = \frac{{70}}{2}\].
\[{M_o} = \frac{{80}}{3}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10
\(\frac{{4\sqrt 2 }}{7}\).
\(\frac{{\sqrt 5 }}{2}\).
\( - \frac{{4\sqrt 2 }}{7}\).
\( - \frac{{\sqrt 5 }}{2}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11
\(y = {\tan ^2}x\).
\(y = \cos 3x \cdot \sin x\).
\(y = \cos x + \sin x\).
\(y = \cos x \cdot {\sin ^2}x\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.


![Cho mẫu số liệu ghép nhóm về chiều cao của \[25\]cây dừa giống, như sau:
Mốt của mẫu số liệu ghép nhóm này là (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/blobid2-1757597535.png)

