20 câu trắc nghiệm Toán 11 Kết nối tri thức Giới hạn của dãy số có đáp án
38 người thi tuần này 4.6 625 lượt thi 20 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 10
Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 8
Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 7
Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 6
Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 5
Bộ 10 đề thi Cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 4
Bộ 10 đề thi cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 2
Bộ 10 đề thi cuối kì 2 Toán 11 Chân trời sáng tạo có đáp án - Đề 1
Danh sách câu hỏi:
Lời giải
Ta có \[{\rm{0}} \le \left| {\frac{{{\rm{sin5n}}}}{{{\rm{3n}}}}} \right| \le \frac{{\rm{1}}}{{\rm{n}}}\] mà \[\lim \frac{1}{{\rm{n}}} = 0\]
Nên theo nguyên lý kẹp có: \[{\mathop{\rm li}\nolimits} {\rm{m}}\,\frac{{{\rm{sin5n}}}}{{{\rm{3n}}}}{\rm{ = 0}}\] do đó \[\mathop {\lim }\limits_{} \left( {\frac{{{\rm{sin5n}}}}{{{\rm{3n}}}} - 2} \right) = - 2\]
Đáp án cần chọn là: A
Lời giải
Ta có 
Đáp án cần chọn là: D
Lời giải

Đáp án cần chọn là: B
Lời giải
Ta có 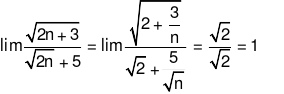 Đáp án cần chọn là: B
Đáp án cần chọn là: B
Lời giải
Ta có \[{\rm{C}}_{\rm{n}}^{\rm{2}}{\rm{ < }}{{\rm{2}}^{\rm{n}}}\]
Khi \[{\rm{n}} \to \infty \Rightarrow {2^{\rm{n}}} < {3^{\rm{n}}}\] do đó \[{\rm{C}}_{\rm{n}}^{\rm{2}}{\rm{ < }}{{\rm{3}}^{\rm{n}}} \Rightarrow \frac{{{\rm{n}}\left( {{\rm{n}} - {\rm{1}}} \right)}}{{\rm{2}}}{\rm{ < }}{{\rm{3}}^{\rm{n}}}\]
Ta có
\[ \Rightarrow \lim \sqrt {{{2.3}^{\rm{n}}} - {\rm{n}} + 2} = + \infty \]
Đáp án cần chọn là: D
Câu 6
A. 1
B. 0
C. 2
D. 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \[\lim {{\rm{u}}_{\rm{n}}}{\rm{ = 0}}\] nếu \[\left| {{{\rm{u}}_{\rm{n}}}} \right|\]có thể nhỏ hơn môt số dương bé tùy ý, kể từ một số hạng nào đó trở đi
B. \[\lim {{\rm{u}}_{\rm{n}}}{\rm{ = 0}}\]nếu \[\left| {{{\rm{u}}_{\rm{n}}}} \right|\]có thể lớn hơn môt số dương bé tùy ý, kể từ một số hạng nào đó trở đi
C. \[\lim {{\rm{u}}_{\rm{n}}}{\rm{ = 0}}\]nếu un có thể nhỏ hơn môt số dương bé tùy ý, kể từ một số hạng nào đó trở đi
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 8
A. 10
B. 8
C. 6
D. 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 9
A. 1
B. 4
C. 3
D. 2
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18
A. \[{\rm{S}} = {\sin ^2}{\rm{x}}\]
B. \[{\rm{S}} = {\cos ^2}{\rm{x}}\]
C. \[{\rm{S}} = \frac{1}{{\sin {\rm{x}}}}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19
A. 17
B. 68
C. 133
D. 137
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

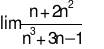 bằng:
bằng:
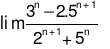 bằng:
bằng: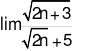 bằng:
bằng:

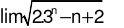 bằng:
bằng:
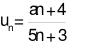 trong đó a là tham số thực. Để dãy số có giới hạn bằng 2, giá trị của a là
trong đó a là tham số thực. Để dãy số có giới hạn bằng 2, giá trị của a là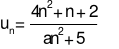 trong đó a là tham số thực. Để dãy số có giới hạn bằng 2, giá trị của a là
trong đó a là tham số thực. Để dãy số có giới hạn bằng 2, giá trị của a là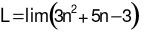


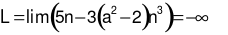
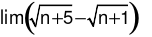 bằng
bằng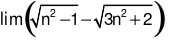 bằng
bằng

 là:
là:



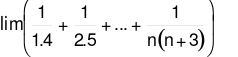 là:
là:
 bằng:
bằng:

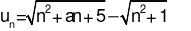 , trong đó a là tham số thực. Tìm a để
, trong đó a là tham số thực. Tìm a để 
 . Tính tổng
. Tính tổng 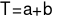
 độ cao của lần rơi trước. Giả sử quả bóng luôn chuyển động vuông góc với mặt đất. Tổng quãng đường bóng đã di chuyển (từ lúc bắt đầu thả đến lúc bóng không di chuyển nữa) gần nhất với kết quả nào sau đây?
độ cao của lần rơi trước. Giả sử quả bóng luôn chuyển động vuông góc với mặt đất. Tổng quãng đường bóng đã di chuyển (từ lúc bắt đầu thả đến lúc bóng không di chuyển nữa) gần nhất với kết quả nào sau đây?