1. Lớp 11
  2. Toán
  3. Đề kiểm tra Hai đường thẳng song song (có lời giải)

Đề kiểm tra Hai đường thẳng song song (có lời giải) - Đề 1

51 người thi tuần này 4.6 626 lượt thi 22 câu hỏi 45 phút

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

🔥 Học sinh cũng đã học

46 người thi tuần này

Đề cương ôn tập cuối kì 2 Toán 11 Chân trời sáng tạo cấu trúc mới có đáp án - Tự luận

274 lượt thi 18 câu hỏi
41 người thi tuần này

Đề cương ôn tập cuối kì 2 Toán 11 Chân trời sáng tạo cấu trúc mới có đáp án - Xác suất

269 lượt thi 32 câu hỏi
44 người thi tuần này

Đề cương ôn tập cuối kì 2 Toán 11 Chân trời sáng tạo cấu trúc mới có đáp án - Quan hệ vuông góc trong không gian

272 lượt thi 50 câu hỏi
35 người thi tuần này

Đề cương ôn tập cuối kì 2 Toán 11 Chân trời sáng tạo cấu trúc mới có đáp án - Đạo hàm

263 lượt thi 35 câu hỏi
62 người thi tuần này

Đề cương ôn tập cuối kì 2 Toán 11 Chân trời sáng tạo cấu trúc mới có đáp án - Hàm số mũ và hàm số lôgarit

290 lượt thi 40 câu hỏi
35 người thi tuần này

Đề cương ôn tập cuối kì 2 Toán 11 Cánh diều cấu trúc mới có đáp án - Tự luận

325 lượt thi 19 câu hỏi
53 người thi tuần này

Đề cương ôn tập cuối kì 2 Toán 11 Cánh diều cấu trúc mới có đáp án - Quan hệ vuông góc trong không gian. Phép chiếu vuông góc

343 lượt thi 50 câu hỏi
43 người thi tuần này

Đề cương ôn tập cuối kì 2 Toán 11 Cánh diều cấu trúc mới có đáp án - Đạo hàm

333 lượt thi 35 câu hỏi

Danh sách câu hỏi:

Câu 1/22

Phần 1. Câu hỏi trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi, thí sinh chỉ chọn 1 phương án.

Cho hình chóp S.ABCD) có đáy ABCD là hình bình hành. Gọi \(I,J,E,F\) lần lượt là trung điểm SA,SB,SC,SD. Trong các đường thẳng sau, đường thẳng nào không song song với \[IJ?\]              
A. \(AD\).                  
B. \(DC\).                
C. \(EF\).                        
D. \(AB\).

Lời giải

Chọn A

Chọn A Vì \(AD\;{\rm{//}}\;IF\) nên \(AD\) không song song với \[IJ\]. (ảnh 1)

Vì \(AD\;{\rm{//}}\;IF\) nên \(AD\) không song song với \[IJ\].

Câu 2/22

Cho hình chóp tứ giác S.ABCD, gọi \(M\) và \(N\) lần lượt là trung điểm các cạnh \(SA\) và \(SC.\) Khi đó \(MN\) song song với đường thẳng              

A. \(AC.\)                  
B. \(BC.\)                
C. \(CD.\)                       
D. \(AD.\)

Lời giải

Chọn A

Do \(MN\) là đường trung bình của tam giác \(SAC\) nên \(MN{\rm{//}}AC.\).

Câu 3/22

Cho hình chóp S.ABCD có ABCD là hình bình hành. Gọi \(I,J,E,F\) lần lượt là trung điểm SA,SB,SC,SD. Trong các đường thẳng sau, đường thẳng nào không song song với \[{\rm{IJ}}\]?              

A. \(EF\).                   
B. \(DC\).                
C. \(AD\).                       
D. \(AB\).

Lời giải

Chọn C

Chọn C Xét \[\Delta SAB\], \[IJ\] là dường trung bình \( \Rightarrow IJ//AB\) mà \(AB//CD\) \( \Rightarrow IJ//CD\). Xét \[\Delta SCD\], \[EF\] là dường trung bình \( \Rightarrow EF//\,CD\) \( \Rightarrow IJ//\,EF\). (ảnh 1)

Xét \[\Delta SAB\], \[IJ\] là dường trung bình \( \Rightarrow IJ//AB\) mà \(AB//CD\) \( \Rightarrow IJ//CD\).

Xét \[\Delta SCD\], \[EF\] là dường trung bình \( \Rightarrow EF//\,CD\) \( \Rightarrow IJ//\,EF\).

Câu 4/22

Cho tứ diện ABCD,\[G\]là trọng tâm tứ diện.Gọi\({G_1}\)là giao điểm của\[AG\]và mp\[\left( {BCD} \right)\],\({G_2}\)là giao điểm của\[BG\] và mp\[\left( {ACD} \right)\].Khẳng định nào sau đây là đúng?              

A. \({G_1}{G_2}\,{\rm{//}}\,AB\).          
B. \({G_1}{G_2}\,{\rm{//}}\,AC\).               
C. \({G_1}{G_2}\,{\rm{//}}\,CD\).               
D. \({G_1}{G_2}\,{\rm{//}}\,AD\).

Lời giải

Chọn A

tâm của tam giác do đó \[\frac{{{G_2}M}}{{{G_2}A}} = \frac{1}{2}\].Tương tự ta cũng có \[\frac{{{G_1}M}}{{{G_1}B}} = \frac{1}{2}\]suy ra\({G_1}{G_2}\,{\rm{//}}\,AB\). (ảnh 1)

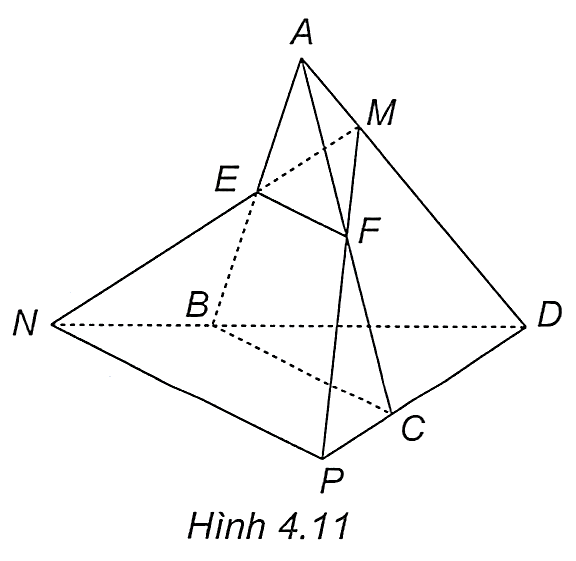
Gọi\[M\],\[N\]lần lượt là trung điểm của \[DC\],\[AC\].Vì\[G\]là trọng tâm tứ diện nên\[G\]là giao điểm của ba đoạn thẳng nối hai trung điểm của cặp cạnh đối của tứ diện như hình vẽ trên.

Xét\[\left( {ABM} \right)\]:\[AG \cap BM = {G_1}\],\[BG \cap AM = {G_2}\].Trong\[\Delta ACD\]có\[AM\]và\[DN\]là đường trung tuyến nên\({G_2}\)là trọng tâm của tam giác do đó \[\frac{{{G_2}M}}{{{G_2}A}} = \frac{1}{2}\].Tương tự ta cũng có \[\frac{{{G_1}M}}{{{G_1}B}} = \frac{1}{2}\]suy ra\({G_1}{G_2}\,{\rm{//}}\,AB\).

Câu 5/22

Cho tứ diện ABCD.Gọi\(I\),\(J\)lần lượt là trọng tâm các tam giác ABC, ABD.Đường thẳng \(IJ\)song song với đường thẳng              

A. \(AC\).                                                   
B. \(CD\).              
C. \(CM\) với\(M\) là trung điểm cạnh\(BD\).                
D. \(DB\).

Lời giải

Chọn B

Cho tứ diện\(ABCD\).Gọi\(I\),\(J\)lần lượt là trọng tâm các tam giác\(ABC\),\(ABD\).Đường thẳng \(IJ\)song song với đường thẳng A. \(AC\). B. \(CD\). C. \(CM\) với\(M\) là trung điểm cạnh\(BD\). D. \(DB\). (ảnh 1)

Gọi\(M\),\(N\)lần lượt là trung điểm của các cạnh\(BD\)và\(BC\),ta có\(MN{\rm{//}}CD\).

Vì\(I,J\)lần lượt là trọng tâm các tam giác\(ABC\),\(ABD\) nên ta có

\(\frac{{AI}}{{AN}} = \frac{{AJ}}{{AM}} = \frac{2}{3}\)\( \Rightarrow IJ{\rm{//}}MN\).

Từ và suy ra\(IJ{\rm{//}}CD\).

Câu 6/22

Cho tứ diện ABCD. Gọi\(I\)và\(J\)lầnl ượt là trọng tâm\(\Delta ABC\)và\(\Delta ABD\).                Chọn khẳng định đúng.              

A. \(IJ\)song songvới\(CD\).                     
B. \(IJ\)song songvới\(AB\).              
C. \(IJ\)chéo nhauvới\(CD\).                     
D. \(IJ\)cắt\(AB\).

Lời giải

Chọn A

Cho tứ diện\(ABCD\).Gọi\(I\)và\(J\)lầnl ượt là trọng tâm\(\Delta ABC\)và\(\Delta ABD\). Chọn khẳng định đúng. A. \(IJ\)song songvới\(CD\). B. \(IJ\)song songvới\(AB\). C. \(IJ\)chéo nhauvới\(CD\). D. \(IJ\)cắt\(AB\). (ảnh 1)

Gọi\(E\)là trung điểm\(AB\).

Vì\(I\)và\(J\)lần lượt là trọng tâm tam giác\(ABC\)và\(ABD\)nên:\(\frac{{EI}}{{EC}} = \frac{{EJ}}{{ED}} = \frac{1}{3}\).

Suyra:\(IJ//CD\).

Câu 7/22

Cho hình chóp S.ABC có \[E,{\rm{ }}F\]lần lượt là trung điểm cạnh \[AB,{\rm{ }}BC\]và điểm \[G\]thỏa mãn \[\overrightarrow {SG} = \frac{1}{2}\overrightarrow {SC} \]. Thiết diện của hình chóp \[S.ABC\]khi cắt bởi mặt phẳng \[\left( {EFG} \right)\]là hình nào dưới đây?              

A. Tam giá.              
B. Hình bình hành.              
C. Hình thang chỉ có một cặp cạnh song song.              
D. Hình thoi.

Lời giải

Cho hình chóp \[S.ABC\]có \[E,{\rm{ }}F\]lần lượt là trung điểm cạnh \[AB,{\rm{ }}BC\]và điểm \[G\]thỏa mãn \[\overrightarrow {SG} = \frac{1}{2}\overrightarrow { (ảnh 1)

Chọn B

Ta có \[EF\]là đường trung bình trong tam giác \[ABC,\]suy ra \[EF//AC{\rm{  }}\left( 1 \right)\].

\[\left. \begin{array}{l}\left( {EFG} \right) \cap \left( {SAC} \right) = \left\{ G \right\}\\EF \subset \left( {EFG} \right)\\AC \subset \left( {SAC} \right)\\EF//AC\end{array} \right\} \Rightarrow \]\[\left( {EFG} \right) \cap \left( {SAC} \right) = Gx//FE//AC\]

Gọi \[Gx \cap SA = \left\{ H \right\}\], suy ra \[H\]là trung điểm \[SA\]và \[HG//AC{\rm{     }}\left( 2 \right)\]

Ta có \[\overrightarrow {SG}  = \frac{1}{2}\overrightarrow {SC} ,\]suy ra \[G\]là trung điểm của \[SC\]và \[GF//SB{\rm{       }}\left( 3 \right)\].

Ta có \[HE\]là đường trung bình trong tam giác \[SAB,\]suy ra \[HE//SB{\rm{       }}\left( 4 \right)\]

Từ \[\left( 1 \right),\left( 2 \right),\left( 3 \right),\left( 4 \right)\]suy ra thiết diện là hình bình hành \[FGHE\].

Câu 8/22

Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi \(M,{\rm{ }}N\) lần lượt là trung điểm \(SA,{\rm{ }}SB\). \(P\) là một điểm trên cạnh \(BC\). Thiết diện tạo bởi mặt phẳng \(\left( {MNP} \right)\) với hình chóp có dạng là:              

A. Hình chữ nhật.      
B. Hình thang.              
C. Hình tam giác.      
D. Hình bình hành.

Lời giải

Chọn B

Chọn B Do \(MN//AB\) và \(MN = \frac{1}{2}AB\) nên \(\left( {MNP} \right) \cap \left( {ABCD} \right) = PQ\) với \(PQ//AB,{\rm{ }}Q \in AD\). Tứ giác \(MNPQ\) là hình thang. (ảnh 1)

Do \(MN//AB\) và \(MN = \frac{1}{2}AB\) nên \(\left( {MNP} \right) \cap \left( {ABCD} \right) = PQ\) với \(PQ//AB,{\rm{ }}Q \in AD\).

Tứ giác \(MNPQ\) là hình thang.

Câu 9/22

Cho t diện ABCD. Gọi \[N\] và \[P\] lần lượt là trung điểm của các cạnh \[BD\] và \[AD\]; \[M\] là điểm thuộc đoạn \[BC\] sao cho \[MC = 2MB\]. Kết luận nào sau đây đúng nhất về thiết diện của mặt phẳng \[\left( {MNP} \right)\] với hình chóp \[ABCD\]?             

A. Thiết diện là ngũ giác.                          
B. Thiết diện là hình bình hành.              
C. Thiết diện là hình thang.                       
D. Thiết diện là t giác.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10/22

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm \(O\). Gọi \(I\) là điểm trên cạnh \(SO\). Mặt phẳng \(\left( {ICD} \right)\) cắt hình chóp theo thiết diện là hình gì?              

A. Tam giác.              
B. Hình thang.              
C. Hình bình hành.   
D. Hình chữ nhật.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 11/22

Cho tứ diện ABCD. Gọi \(M\)và \(N\)lần lượt là trung điểm của \(AB\)và \(AC\). \(E\)là điển trên cạnh \(CD\)với \[ED = 3EC\]. Thiết diện tạo bởi mặt phẳng \(\left( {MNE} \right)\)và tứ diện \[ABCD\]là:              

A. Tam giác \(MNE\).              
B. Tứ giác \(MNEF\)với \(F\)là điểm bất kì trên cạnh \(BD\).              
C. Hình bình hành \(MNEF\)với \(F\)là điểm bất kì trên cạnh \(BD\)mà \[EF\]song song với \(BC\)              
D. Hình thang \(MNEF\)với \(F\)là điểm trên cạnh \(BD\)mà \[EF\]song song với \(BC\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 12/22

Cho hình chóp tứ giác S.ABCD có đáy ABCD là hình bình hành. Gọi \[I\] là trung điểm \[SA\]. Thiết diện của hình chóp c      ắt bởi mặt phẳng \[\left( {IBC} \right)\] là              

A. Tam giác \[IBC\].              
B. Hình thang \[IBCJ\] (\[J\] là trung điểm \[SD\]).              
C. Hình thang \[IGBC\] (\[G\] là trung điểm \[SB\]).              
D. Tứ giác \[IBCD\].

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 13/22

Phần 2. Trắc nghiệm lựa chọn đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Trong các mệnh đề sau, mệnh đề nào đúng?

a) Hai đường thẳng không có điểm chung là hai đường thẳng song song hoặc chéo nhau.

b) Hai đường thẳng chéo nhau khi chúng không có điểm chung.

c) Hai đường thẳng song song khi chúng ở trên cùng một mặt phẳng.

d) Khi hai đường thẳng ở trên hai mặt phẳng thì hai đường thẳng đó chéo nhau.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 14/22

Cho hình chóp S.ABCD có đáy là hình bình hành. Khi đó:

a) \(AB\) song song \(CD\)

b) \(SA\) cắt \(SC\);

c) \(SA\) song song \(BC\).

d) \(SC\) chéo nhau \(AB\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 15/22

Cho hình chóp S.ABCD có đáy là hình bình hành. Điểm \(M\) thuộc cạnh \(SA\), điểm \(E\) và \(F\) lần lượt là trung điểm của \(AB\) và \(BC\). Khi đó:

a) \(EF//AC\)

b) Giao tuyến của hai mặt phẳng \((SAB)\) và \((SCD)\) là đường thẳng qua \(S\) và song song với \(AC\).

c) Giao tuyến của hai mặt phẳng \((MBC)\) và \((SAD)\) đường thẳng qua \(M\) và song song với \(BC\).

d) Giao tuyến của hai mặt phẳng \((MEF)\) và \((SAC)\) là đường thẳng qua \(M\)và song song với \(AC\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 16/22

Cho tứ diện ABCD, gọi \(I\) và \(J\) lần lượt là trung điểm của \(AD\) và \(AC,G\) là trọng tâm của tam giác \(BCD\).

a) \(IJ//CD\)

b) Giao tuyến của hai mặt phẳng \((GIJ)\) và \((BCD)\) là đường thẳng qua \(G\) và song song với \(BC\)

c) Cho biết \(CD = 6\). Biết \((GIJ)\) cắt \(BC,BD\) lần lượt tại \(M\) và \(N\). Khi đó \(2IJ + 3MN = 17\).

d) Cho biết \(CD = 6\). Biết \((GIJ)\) cắt \(BC,BD\) lần lượt tại \(M\) và \(N\). Khi đó \(3IJ + 2MN = 18\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 17/22

Phần 3. Câu hỏi trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.

Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng. Gọi \(G,H\) lần lượt là giao điểm của hai đường chéo của hai hình bình hành đó. Chứng minh rằng ba đường thẳng \(GH,CE,DF\) đôi một song song.

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 18/22

Cho tứ diện ABCD. Gọi \(M,N\) lần lượt là trung điểm của các cạnh \(AB,AD\) và \(P\) là một điểm nằm trên \(CD\). Đường thẳng \(BC\) cắt mặt phẳng \((MNP)\) tại \(Q\). Chứng minh rằng \(PQ//BD\)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 19/22

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi \(I,J\) lần lượt là trung điểm của các cạnh \(SA\) và \(SB\). Chứng minh rằng \(IJ//AB\), từ đó suy ra \(IJ//CD\).

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 20/22

Cho tứ diện ABCD. Gọi \(E,F\) lần lượt là trung điểm của các cạnh \(AB,AC\) và \(M\) là một điểm bất kì thuộc cạnh \(AD\). Giả sử \(ME\) cắt \(BD\) tại \(N\) và \(MF\) cắt \(CD\) tại \(P(H.4.11)\). Chứng minh rằng \(NP//EF\).

Cho tứ diện \(ABCD\). Gọi \(E,F\) lần lượt là trung điểm của các cạnh \(AB,AC\) và \(M\) là một điểm bất kì thuộc cạnh \(AD\). Giả sử \(ME\) cắt \(BD\) tại \(N\) và \(MF\) cắt \(CD\) tại \(P(H.4.11)\). Chứng minh rằng \(NP//EF\). (ảnh 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Xem tiếp với tài khoản VIP

Còn 14/22 câu hỏi, đáp án và lời giải chi tiết.

Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Đăng ký

Bạn đã có tài khoản?

CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
Giấy chứng nhận ĐKKD số: 0108307822 do Sở KH & ĐT TP Hà Nội cấp lần đầu ngày 04/06/2018
© 2017 Vietjack37. All Rights Reserved.
zalo Nhắn tin Zalo Hỏi bài tập