$Chọn A Gọi \[M,\,N\] lần lượt là trung điểm của \[BC,\,BD\], ta có \[MN//CD\] (1) Xét \[\Delta AMN\] có \[\frac{{AI}}{{AM}} = \frac{{AJ}}{{AN}} = \frac{2}{3}\]\[ \Rightarrow IJ//MN\] (2) Từ (1) và (2) suy ra \[IJ//CD\]. (ảnh 1)$

Gọi \[M,\,N\] lần lượt là trung điểm của \[BC,\,BD\], ta có \[MN//CD\] (1)

Xét \[\Delta AMN\] có \[\frac{{AI}}{{AM}} = \frac{{AJ}}{{AN}} = \frac{2}{3}\]\[ \Rightarrow IJ//MN\] (2)

Từ (1) và (2) suy ra \[IJ//CD\].

Câu 2

Cho hình chóp S.ABCD. Gọi M,N,P,Q,R,T lần lượt là trung điểm AC,BD,BC,CD,SA,SD. Cặp đường thẳng nào sau đây song song với nhau?

A. $MP$ và $RT$.

B. $MQ$ và $RT$.

C. $MN$ và $RT$.

D. $PQ$ và $RT$.

Lời giải

Chọn B

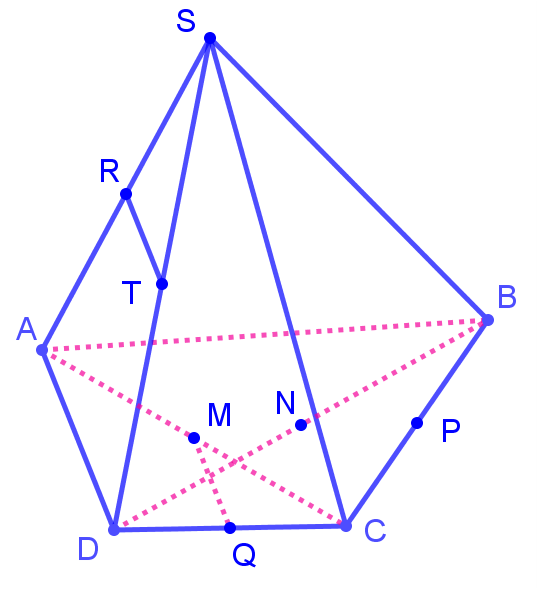
$Cho hình chóp $S.ABCD$. Gọi $M,N,P,Q,R,T$ lần lượt là trung điểm $AC,BD,BC,CD,SA,SD$. Cặp đường thẳng nào sau đây song song với nhau? A. $MP$ và $RT$. B. $MQ$ và $RT$. C. $MN$ và $RT$. D. $PQ$ và $RT$. (ảnh 1)$

Xét \[\Delta SAD\] có \[RT\] là đường trung bình của tam giác \[ \Rightarrow RT//AD\] (1)

Xét \[\Delta ACD\] có \[MQ\] là đường trung bình của tam giác \[ \Rightarrow MQ//AD\] (2)

Từ (1) và (2) \[ \Rightarrow MQ//RT\].

Câu 3

Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và \[M\] là trung điểm cạnh \[SC\]. Khi đó thiết diện của hình chóp khi cắt bởi mặt phẳng \[\left( {MAB} \right)\] là

A. một tam giác.

B. một hình thang.

C. một hình bình hành.

D. một hình ngũ giác.

Lời giải

Chọn B

$Khi đó thiết diện của hình chóp khi cắt bởi mặt phẳng \[\left( {MAB} \right)\] là một hình thang. (ảnh 1)$

Ta có \[\left( {ABCD} \right) \cap \left( {SCD} \right) = CD\]; \[\left( {ABCD} \right) \cap \left( {MAB} \right) = AB\]; \[\left( {MAB} \right) \cap \left( {SCD} \right) = d\] và \[AB\,{\rm{//}}\,CD\]nên \[AB\,\,;\,\,CD\,\,;\,\,d\] đôi một song song \[\left( 1 \right)\].

Mặt khác \[M\]là điểm chung của \[\left( {MAB} \right);\,\,\left( {SCD} \right)\] \[\left( 2 \right)\].

Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] suy ra \[d\] đi qua\[M\] và song song với \[CD\], cắt \[SD\]tại \[N\].

Khi đó thiết diện của hình chóp khi cắt bởi mặt phẳng \[\left( {MAB} \right)\] là một hình thang.

Câu 4

Cho tứ diện ABCD. $M$ là một điểm bất kỳ nằm trên đoạn $AC$ (khác $A,C$). Mặt phẳng $\left( P \right)$ qua $M$ và song song với các đường thẳng $AB,CD$. Thiết diện của $\left( P \right)$ với tứ diện đã cho là hình gì?

A. Hình chữ nhật.

B. Hình thang.

C. Hình vuông.

D. Hình bình hành.

Lời giải

Chọn D

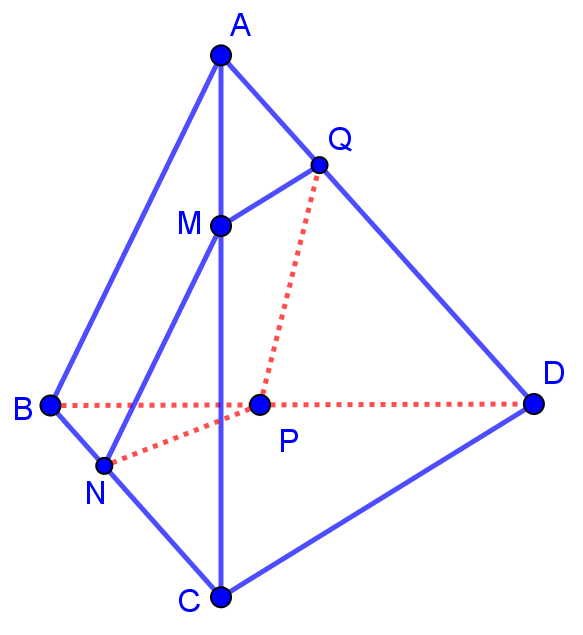
$Mặt khác \[\left\{ \begin{array}{l}MQ//NP\,\,\left( {//CD} \right)\\MN//PQ\,\,\,\left( {//AB (ảnh 1)$

Trong mp \[\left( {ABC} \right)\], qua $M$ kẻ đường thẳng song song với \[AB\], cắt \[BC\] tại \[N\]

Trong mp \[\left( {ACD} \right)\], qua $M$ kẻ đường thẳng song song với \[CD\], cắt \[AD\] tại \[Q\]

Trong mp \[\left( {BCD} \right)\], qua $M$ kẻ đường thẳng song song với \[CD\], cắt \[BD\] tại \[P\]

\[ \Rightarrow \] Thiết diện của $\left( P \right)$ với tứ diện là tứ giác \[MNPQ\].

Mặt khác \[\left\{ \begin{array}{l}MQ//NP\,\,\left( {//CD} \right)\\MN//PQ\,\,\,\left( {//AB} \right)\end{array} \right.\]\[ \Rightarrow MNPQ\] là hình bình hành.

Câu 5

Cho tứ diện ABCD. Gọi \[M\], \[N\] lần lượt là trung điểm của \[AB\] và \[AC\]. \[E\] là điểm trên cạnh \[CD\] và \[ED = 3EC\]. Thiết diện tạo bởi mặt phẳng \[\left( {MNE} \right)\] và tứ diện \[ABCD\] là

A. Tam giác \[MNE\].

B. Tứ giác \[MNEF\] với \[F\] là điểm bất kì trên cạnh \[BD\].

C. Hình bình hành \[MNEF\] với \[F\] là điểm trên cạnh \[BD\] mà \[EF\,{\rm{//}}\,BC\].

D. Hình thang \[MNEF\] với \[F\] là điểm trên cạnh \[BD\] mà \[EF\,{\rm{//}}\,BC\].

Lời giải

Chọn D

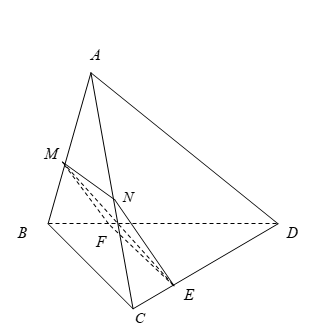
$Do đó thiết diện tạo bởi mặt phẳng \[\left( {MNE} \right (ảnh 1)$

Xét hai mặt phẳng \[\left( {MNE} \right)\] và \[\left( {BCD} \right)\], có;

\[E \in \left( {MNE} \right) \cap \left( {BCD} \right)\]

Và \[MN\,{\rm{//}}\,BC\] (\[MN\]là đường trung bình của \[\Delta ABC\]), \[MN \subset \left( {MNE} \right),\,BC \subset \left( {BCD} \right)\]

Nên \[\left( {MNE} \right) \cap \left( {BCD} \right) = EF\]\[\left( {EF\,{\rm{//}}\,MN\,{\rm{//}}\,BC,\,F = BD \cap EF} \right)\].

Do đó thiết diện tạo bởi mặt phẳng \[\left( {MNE} \right)\] và tứ diện \[ABCD\] là hình thang\[MNEF\](\[MN\,{\rm{//}}\,EF\]).

Câu 6

Cho tứ diện ABCD. Gọi $I,J$lần lượt là trọng tâm của tam giác ABC, ABD. Tìm khẳng định đúng trong các khẳng định sau đây.

A. Hai đường thẳng \[IJ\]và $CD$cắt nhau.

B. Hai đường thẳng \[IJ\]và $CD$chéo nhau.

C. Hai đường thẳng \[IJ\]và $CD$song song nhau và \[IJ = \frac{1}{3}CD\].

D. Hai đường thẳng \[IJ\]và $CD$song song nhau và \[IJ = \frac{2}{3}CD\].

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Tiếng Anh

Giáo dục Kinh tế và Pháp luật

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Viên chức

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Global success

iLearn Smart World

Friends Global

Bright

Explore new worlds

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Toán

Vật lý

Hóa học