Cho hình bình hành \[ABCD\] có \[AC \bot AD\] và \(AD = 3,5\,;\,\,\widehat D = 50^\circ \). Hỏi diện tích của hình bình hành là bao nhiêu? (Kết quả làm tròn đến hàng phần mười)
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án đúng là: B
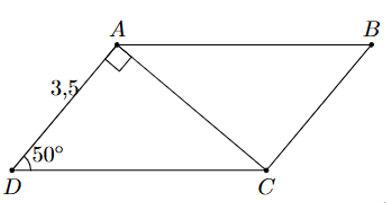
Xét \[\Delta ADC\] vuông tại \[A,\] ta có: \(AC = AD \cdot \tan \widehat {ADC} = {\rm{ }}3,5 \cdot \tan \,50^\circ .\)
Khi đó gọi S là diện tích hình bình hành, ta có:
\[S = AD \cdot AC = 3,5 \cdot 3,5\tan 50^\circ \approx 14,6.\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Gọi \(x\) là số trận thắng – thua và \(y\) là số trận hòa \[\left( {x,{\rm{ }}y \in \mathbb{N}*} \right)\].
Nếu có 5 đội tham gia thi đấu, mỗi đội phải đấu với 4 đội còn lại nên với 5 đội tham gia thì có \(5 \cdot 4 = 20\) (trận đấu). Nhưng mỗi trận đấy có 2 đội tham gia nên tổng số trận đấu khi có 5 đội tham gia là \(\frac{{5 \cdot 4}}{2} = 10\) (trận đấu).
Vì có 10 trận đấu nên
Mặt khác, tổng số điểm các đội là \(10 + 9 + 6 + 4 + 0 = 29\) (điểm).
Mỗi trận thắng – thua có tổng số điểm là 3 và mỗi trận hòa có tổng số có tổng số điểm là 2 nên ta có phương trình \(3x + 2y = 29\) \[\left( 2 \right)\]
Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] ta có hệ phương trình
Từ phương trình thứ hai ta có \(x + y = 10\) suy ra \(x = 10 - y\). Thế vào phương trình thứ nhất, ta được:
\(3\left( {10 - y} \right) + 2y = 29\), suy ra \(30 - 3y + 2y = 29\) hay \(y = 1\) (thỏa mãn).
Từ đó \(x = 10 - y = 10 - 1 = 9\) (thỏa mãn).
Mỗi đội có 4 trận đấu với các đội còn lại mà đội A có 10 điểm tức đội A thắng 3 trận hòa 1 trận.
Đội B có 9 điểm tức thắng 3 trận thua 1 trận.
Đội C có 6 điểm tức thắng 2 trận thua 2 trận.
Đội D có 4 điểm thắng 1 trận hòa 1 trận.
Đội E không có điểm tức là thua hết 4 trận.
Vậy trận hòa là của đội A và đội D.
Câu 2
Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)
Giải hệ phương trình \[\left\{ \begin{array}{l}6x - 3y = - 12\,\,\,\left( 1 \right)\\ - 2x + y = 4\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\] bằng phương pháp thế theo các bước:
a) Từ phương trình (2), ta có \(y = 2x + 4\).
b) Thay \(y = 2x + 4\) vào phương trình (1), ta được \(0x = 0\).
c) Phương trình \(0x = 0\) vô nghiệm.
d) Nghiệm tổng quát của hệ phương trình đã cho là \(\left( {2y + 4;\,\,y} \right)\) với \(x \in \mathbb{R}\) tùy ý.
Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)
Giải hệ phương trình \[\left\{ \begin{array}{l}6x - 3y = - 12\,\,\,\left( 1 \right)\\ - 2x + y = 4\,\,\,\,\,\,\,\,\left( 2 \right)\end{array} \right.\] bằng phương pháp thế theo các bước:
a) Từ phương trình (2), ta có \(y = 2x + 4\).
b) Thay \(y = 2x + 4\) vào phương trình (1), ta được \(0x = 0\).
c) Phương trình \(0x = 0\) vô nghiệm.
d) Nghiệm tổng quát của hệ phương trình đã cho là \(\left( {2y + 4;\,\,y} \right)\) với \(x \in \mathbb{R}\) tùy ý.
Lời giải
Hướng dẫn giải
Đáp án: a) Đúng. b) Đúng. c) Sai. d) Sai.
Giải hệ phương trình đã cho bằng phương pháp thế như sau:
• Từ phương trình (2), ta có \(y = 2x + 4\).
• Thay \(y = 2x + 4\) vào phương trình (1), ta được:
\(6x - 3\left( {2x + 4} \right) = - 12\) hay \(0x = 0\).
• Phương trình trên có vô số nghiệm nên hệ phương trình đã cho có vô số nghiệm.
• Nghiệm tổng quát của hệ phương trình đã cho là \(\left( {x;\,\,2x + 4} \right)\) với \(x \in \mathbb{R}\) tùy ý.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.