B. TỰ LUẬN (3,0 điểm)
(1,0 điểm) Giải bài toán sau bằng cách lập hệ phương trình:
Người ta cho thêm \[1\] kg nước vào dung dịch \[A\] (của axit \(X)\) thì được dung dịch \[B\] có nồng độ axit là \[20\% \]. Sau đó lại cho thêm \[1\] kg axit \(X\) vào dung dịch \[B\] thì được dung dịch \[C\] có nồng độ axit là \[33\frac{1}{3}\% \]. Tính nồng độ axit của dung dịch \[A\].
B. TỰ LUẬN (3,0 điểm)
(1,0 điểm) Giải bài toán sau bằng cách lập hệ phương trình:
Người ta cho thêm \[1\] kg nước vào dung dịch \[A\] (của axit \(X)\) thì được dung dịch \[B\] có nồng độ axit là \[20\% \]. Sau đó lại cho thêm \[1\] kg axit \(X\) vào dung dịch \[B\] thì được dung dịch \[C\] có nồng độ axit là \[33\frac{1}{3}\% \]. Tính nồng độ axit của dung dịch \[A\].
Quảng cáo
Trả lời:
Hướng dẫn giải
Gọi \(x{\rm{\;(kg)}}\) là khối lượng axit \(X\) có trong dung dịch \(A\) và \(y{\rm{\;(kg)}}\) là khối lượng dung dịch chất \(A\) \(\left( {y > x > 0} \right)\).
Khi thêm \[1\] kg nước vào dung dịch \[A\] thì được dung dịch \[B\] có khối lượng là: \(y + 1{\rm{\;(kg)}}\).
Theo bài, nồng độ của dung dịch \(B\) là \[20\% \] nên ta có phương trình:
\(\frac{x}{{y + 1}} \cdot 100\% = 20\% \) hay \(5x = y + 1\) suy ra \(5x - y = 1\) (1)
Khi thêm \[1\] kg axit vào dung dịch \[B\] thì được dung dịch \[C\] có khối lượng là: \(y + 1 + 1 = y + 2{\rm{\;(kg)}}\) và khối lượng axit \(X\) có trong dung dịch lúc này là \(x + 1{\rm{\;(kg)}}\)
Theo bài, nồng độ của dung dịch \(C\) là \[33\frac{1}{3}\% \] nên ta có phương trình:
\(\frac{{x + 1}}{{y + 2}} \cdot 100\% = 33\frac{1}{3}\% \) hay \(3\left( {x + 1} \right) = y + 2\) suy ra \(3x - y = - 1\). (2)
Từ phương trình (1) và phương trình (2), ta có hệ phương trình: \(\left\{ \begin{array}{l}5x - y = 1\\3x - y = - 1\end{array} \right.\)
Trừ từng vế phương trình thứ nhất cho phương trình thứ hai của hệ trên, ta được:
\(2x = 2,\) suy ra \(x = 1\) (thỏa mãn).
Thay \(x = 1\) vào phương trình \(5x = y + 1\) ta được:
\(5 \cdot 1 = y + 1\), suy ra \(y = 4\) (thỏa mãn).
Vậy nồng độ axit của dung dịch \(A\) là: \(\frac{x}{y} \cdot 100\% = \frac{1}{4} \cdot 100\% = 25\% .\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)
Giải hệ phương trình \(\left\{ \begin{array}{l}2x - 6y = 5\\2x - 6y = 4.\end{array} \right.\) bằng phương pháp cộng đại số theo các bước:
a) Nhân hai vế của phương trình thứ hai với 2, ta được: \(\left\{ \begin{array}{l}2x - 6y = 5\\2x - 6y = 4.\end{array} \right.\)
b) Trừ từng vế phương trình thứ nhất cho phương trình thứ hai của hệ, ta được \(0x = 1\).
c) Phương trình \(0x = 1\) vô số nghiệm.
d) Nghiệm tổng quát của hệ phương trình đã cho là \(\left( {6y + 5;\,\,2x - 4} \right)\) với \(x \in \mathbb{R}\) tùy ý.
Phần 2. Câu trắc nghiệm đúng sai (2,0 điểm)
Giải hệ phương trình \(\left\{ \begin{array}{l}2x - 6y = 5\\2x - 6y = 4.\end{array} \right.\) bằng phương pháp cộng đại số theo các bước:
a) Nhân hai vế của phương trình thứ hai với 2, ta được: \(\left\{ \begin{array}{l}2x - 6y = 5\\2x - 6y = 4.\end{array} \right.\)
b) Trừ từng vế phương trình thứ nhất cho phương trình thứ hai của hệ, ta được \(0x = 1\).
c) Phương trình \(0x = 1\) vô số nghiệm.
d) Nghiệm tổng quát của hệ phương trình đã cho là \(\left( {6y + 5;\,\,2x - 4} \right)\) với \(x \in \mathbb{R}\) tùy ý.
Lời giải
Hướng dẫn giải
Đáp án: a) Đúng. b) Đúng. c) Sai. d) Sai.
Giải hệ phương trình đã cho bằng phương pháp cộng đại số như sau:
Nhân hai vế của phương trình thứ hai với 2, ta được:
Trừ từng vế phương trình thứ nhất cho phương trình thứ hai của hệ, ta được:
\(0x + 0y = 1\) hay \(0x = 1\).
Phương trình trên vô nghiệm.
Vậy hệ phương trình đã cho vô nghiệm.
Lời giải
Hướng dẫn giải
a) Kẻ \(CH \bot AB,\,\,H \in AB.\) Khi đó \(CH\) là chiều cao của con dốc.
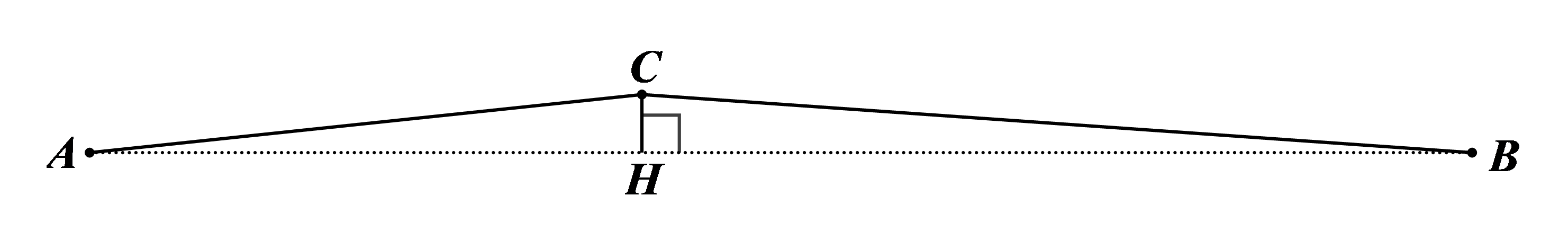
⦁ Xét \(\Delta ACH\) vuông tại \[H,\] ta có: \({\rm{tan}}\widehat {CAH} = \frac{{CH}}{{AH}}\)
Suy ra \(AH = \frac{{CH}}{{{\rm{tan}}\widehat {CAH}}} = \frac{{CH}}{{{\rm{tan6}}^\circ }}\,\,({\rm{m}}).\) (1)
⦁ Xét \(\Delta BCH\) vuông tại \[H,\] ta có: \({\rm{tan}}\widehat {CBH} = \frac{{CH}}{{BH}}\)
Suy ra \(BH = \frac{{CH}}{{{\rm{tan}}\widehat {CBH}}} = \frac{{CH}}{{{\rm{tan4}}^\circ }}\,\,({\rm{m}}).\) (2)
⦁ Từ (1) và (2) ta có: \(AH + BH = \frac{{CH}}{{{\rm{tan6}}^\circ }} + \frac{{CH}}{{{\rm{tan4}}^\circ }}\) hay \(AB = CH \cdot \left( {\frac{1}{{{\rm{tan6}}^\circ }} + \frac{1}{{{\rm{tan4}}^\circ }}} \right)\)
Do đó \(762 = CH \cdot \left( {\frac{1}{{{\rm{tan6}}^\circ }} + \frac{1}{{{\rm{tan4}}^\circ }}} \right)\)
Suy ra \(CH = \frac{{762}}{{\frac{1}{{{\rm{tan6}}^\circ }} + \frac{1}{{{\rm{tan4}}^\circ }}}} \approx 32{\rm{\;(m)}}{\rm{.}}\)
Vậy chiều cao của con dốc là 32 m.
b) ⦁ Xét \(\Delta ACH\) vuông tại \[H,\] ta có: \({\rm{sin}}\widehat {CAH} = \frac{{CH}}{{AC}}\)
Suy ra \(AC = \frac{{CH}}{{{\rm{sin}}\widehat {CAH}}} \approx \frac{{{\rm{32}}}}{{{\rm{sin6}}^\circ }}{\rm{\;(m)}} = \frac{4}{{125{\rm{sin6}}^\circ }}{\rm{\;(km)}}{\rm{.}}\) (3)
Xét \(\Delta BCH\) vuông tại \[H,\] ta có: \({\rm{sin}}\widehat {CBH} = \frac{{CH}}{{CB}}\)
Suy ra \(CB = \frac{{CH}}{{{\rm{sin}}\widehat {CBH}}} \approx \frac{{{\rm{32}}}}{{{\rm{sin4}}^\circ }}{\rm{\;(m)}} = \frac{4}{{125{\rm{sin4}}^\circ }}{\rm{\;(km)}}{\rm{.}}\) (4)
⦁ Thời gian lên dốc \[AC\] là: \[{t_{AC}} = \frac{{{S_{AC}}}}{{{v_{ld}}}} = \frac{{AC}}{{{v_{ld}}}} \approx \frac{4}{{125{\rm{sin6}}^\circ }}:4 = \frac{1}{{125{\rm{sin6}}^\circ }}\] (giờ).
Thời gian xuống dốc \(CB\) là: \[{t_{CB}} = \frac{{{S_{CB}}}}{{{v_{xd}}}} = \frac{{CB}}{{{v_{xd}}}} \approx \frac{4}{{125{\rm{sin4}}^\circ }}:19 = \frac{4}{{{\rm{2}}\,\,{\rm{375sin4}}^\circ }}\] (giờ).
Thời gian đi từ \(A\) đến \(B\) là:
\({t_{AB}} = {t_{AC}} + {t_{CB}} \approx \frac{1}{{125\sin 6^\circ }} + \frac{4}{{{\rm{2}}\,\,{\rm{375sin4}}^\circ }} \approx 0,1007\) (giờ) ≈ 6 phút.
Vậy bạn An đến trường lúc 6 giờ + 6 phút = 6 giờ 6 phút.
Câu 3
Tổng các nghiệm của phương trình \(\left( {\frac{2}{3}x + 6} \right)\left( {8 - 2x} \right) = 0\) là
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
