Phần II. Trắc nghiệm đúng, sai
(Gồm 5 câu hỏi, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d))
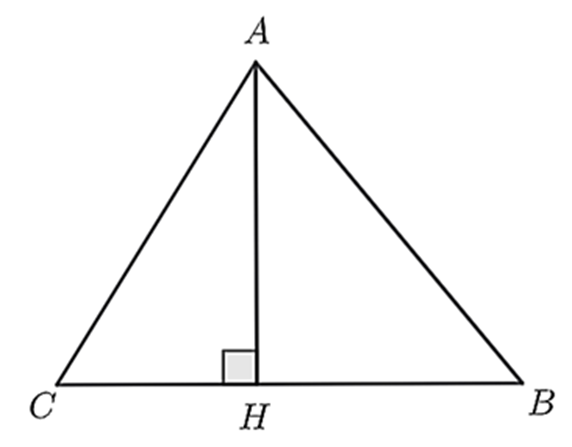
Cho \(\Delta ABC\) có đường cao \(AH.\) Biết rằng \(HB = 4\;{\rm{m}}{\rm{, }}AB = \sqrt {80} \;{\rm{m}}{\rm{,}}\;AC = 10\;{\rm{m}}{\rm{.}}\)
a) \(AH = 8\;{\rm{m}}{\rm{.}}\)
b) \(CH = 9\;{\rm{m}}{\rm{.}}\)
c) Chu vi \(\Delta AHC\) bằng \(40\;{\rm{m}}.\)
d) Chu vi \(\Delta ABC\) lớn hơn chu vi \(\Delta AHC\) khoảng \(15\;{\rm{m}}{\rm{.}}\)
Phần II. Trắc nghiệm đúng, sai
(Gồm 5 câu hỏi, hãy chọn đúng hoặc sai cho mỗi ý a), b), c), d))
Cho \(\Delta ABC\) có đường cao \(AH.\) Biết rằng \(HB = 4\;{\rm{m}}{\rm{, }}AB = \sqrt {80} \;{\rm{m}}{\rm{,}}\;AC = 10\;{\rm{m}}{\rm{.}}\)
a) \(AH = 8\;{\rm{m}}{\rm{.}}\)
b) \(CH = 9\;{\rm{m}}{\rm{.}}\)
c) Chu vi \(\Delta AHC\) bằng \(40\;{\rm{m}}.\)
d) Chu vi \(\Delta ABC\) lớn hơn chu vi \(\Delta AHC\) khoảng \(15\;{\rm{m}}{\rm{.}}\)
Quảng cáo
Trả lời:
a) Đúng.
Vì \(AH\) là đường cao của \(\Delta ABC\) nên \(AH \bot BC.\) Do đó, \(\Delta ABH\) vuông tại \(H.\)
Nên \(A{H^2} + H{B^2} = A{B^2}\) (định lí Pythagore), suy ra \(A{H^2} = A{B^2} - H{B^2} = {\left( {\sqrt {80} } \right)^2} - {4^2} = 64.\)
Suy ra \(AH = \sqrt {64} = 8\;{\rm{m}}{\rm{.}}\) Vậy \(AH = 8\;{\rm{m}}{\rm{.}}\)
b) Sai.
Vì \(AH \bot BC\) nên \(\Delta ACH\) vuông tại \(H.\)
Suy ra \(A{H^2} + H{C^2} = A{C^2}\) (định lí Pythagore), suy ra \(C{H^2} = A{C^2} - A{H^2} = {10^2} - 64 = 36.\)
Suy ra \(CH = \sqrt {36} = 6\;{\rm{m}}{\rm{.}}\) Vậy \(CH = 6\;{\rm{m}}{\rm{.}}\)
c) Sai.
Chu vi \(\Delta AHC\) là: \({P_1} = AH + HC + AC = 8 + 6 + 10 = 24\;\left( {\rm{m}} \right).\)
Vậy chu vi \(\Delta AHC\) bằng \(24\;{\rm{m}}{\rm{.}}\)
d) Sai.
Ta có: \(BC = BH + CH = 4 + 6 = 10\;\left( {\rm{m}} \right).\)
Chu vi \(\Delta ABC\) là: \({P_2} = AC + AB + BC = 10 + \sqrt {80} + 10 = 20 + \sqrt {80} \;\left( {\rm{m}} \right).\)
Ta có: \({P_2} - {P_1} = 20 + \sqrt {80} - 24 = \sqrt {80} - 4 \approx 5\;\left( {\rm{m}} \right).\)
Vậy chu vi \(\Delta ABC\) lớn hơn chu vi \(\Delta AHC\) khoảng \(5\;{\rm{m}}{\rm{.}}\)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
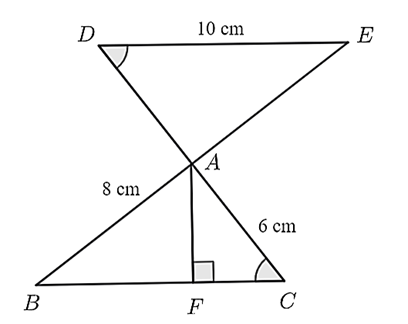
a) Sai.
\(\Delta ADE\) và \(\Delta ACB\) có: \(\widehat D = \widehat C\;\left( {gt} \right),\;AD = AC\;\left( { = 6\;{\rm{cm}}} \right),\;\widehat {DAE} = \widehat {BAC}\) (hai góc đối đỉnh).
Do đó, \(\Delta ADE = \Delta ACB\;\left( {g - c - g} \right).\)
b) Đúng.
Vì \(\Delta ADE = \Delta ACB\;\left( {cmt} \right)\) nên \(DE = BC = 10\;{\rm{cm}}{\rm{.}}\)
Vì: \(A{B^2} + A{C^2} = B{C^2}\;\left( {{\rm{do}}\;{6^2} + {8^2} = {{10}^2}} \right)\) nên \(\Delta ABC\) vuông tại \(A\) (định lí Pythagore đảo).
c) Đúng.
Diện tích \(\Delta ABC\) vuông tại \(A\) là: \(S = \frac{1}{2}AB \cdot AC = \frac{1}{2} \cdot 6 \cdot 8 = 24\;\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
Vậy diện tích \(\Delta ABC\) bằng \(24\;{\rm{c}}{{\rm{m}}^2}.\)
d) Sai.
Vì \(AF\) là đường cao của \(\Delta ABC\) nên diện tích \(\Delta ABC\) là: \(S = \frac{1}{2}AF \cdot BC.\)
Suy ra: \(\frac{1}{2} \cdot AF \cdot 10 = 24,\) suy ra \(AF = 4,8\;{\rm{cm}}{\rm{.}}\)
Lời giải
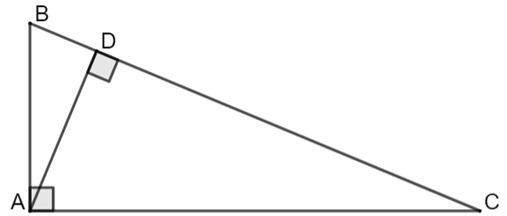
a) Đúng.
Vì tam giác \(ABC\) vuông tại \(A\) nên theo định lí Pythagore ta có:
\(B{C^2} = A{B^2} + A{C^2} = {5^2} + {12^2} = 169\) nên \(BC = \sqrt {169} = 13\;\left( {{\rm{cm}}} \right).\)
Vậy \(BC = 13\;{\rm{cm}}{\rm{.}}\)
b) Sai.
Diện tích \(\Delta ABC\) vuông tại \(A\) là: \(S = \frac{1}{2}AB \cdot AC = \frac{1}{2} \cdot 5 \cdot 12 = 30\;\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
Vậy diện tích \(\Delta ABC\) bằng \(30\;{\rm{c}}{{\rm{m}}^2}.\)
c) Sai.
Vì \(AD\) là đường cao của \(\Delta ABC\) nên diện tích \(\Delta ABC\) là: \(S = \frac{1}{2}AD \cdot BC.\)
Do đó, \(\frac{1}{2} \cdot AD \cdot 13 = 30,\) suy ra \(AD = \frac{{60}}{{13}}\;{\rm{cm}}{\rm{.}}\) Vậy \(AD = \frac{{60}}{{13}}\;{\rm{cm}}{\rm{.}}\)
d) Đúng.
Vì \(\Delta ABD\) vuông tại \(D\) nên theo định lí Pythagore ta có: \(B{D^2} + A{D^2} = A{B^2}\) nên \(B{D^2} + {\left( {\frac{{60}}{{13}}} \right)^2} = {5^2},\) hay \(B{D^2} = \frac{{625}}{{169}},\) suy ra \[BD = \sqrt {\frac{{625}}{{169}}} = \frac{{25}}{{13}}\;\left( {{\rm{cm}}} \right).\]
\(\Delta ABD\) có: \(BD < AD\;\left( {{\rm{Do}}\;\;\frac{{25}}{{13}} < \frac{{60}}{{13}}} \right)\) nên \(\widehat B > \widehat {DAB}.\) Vậy \(\widehat B > \widehat {DAB}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Cho \(\Delta ABC\) cân tại \(A\) có \(AB = 12\;{\rm{cm}}{\rm{, }}BC = 6\;{\rm{cm}}{\rm{.}}\) Gọi \(D\) là trung điểm của \(BC.\) Gọi \(E\) là điểm thuộc tia đối của tia \(DA\) sao cho \(DE = \frac{1}{4}AE.\)
a) \(\Delta ADC\) vuông tại \(D.\)
b) \(AD = \sqrt {135} \;{\rm{cm}}{\rm{.}}\)
c) \(EC = 5\;{\rm{cm}}{\rm{.}}\)
d) Chu vi \(\Delta DEC\) lớn hơn \(12\;{\rm{cm}}{\rm{.}}\)
Cho \(\Delta ABC\) cân tại \(A\) có \(AB = 12\;{\rm{cm}}{\rm{, }}BC = 6\;{\rm{cm}}{\rm{.}}\) Gọi \(D\) là trung điểm của \(BC.\) Gọi \(E\) là điểm thuộc tia đối của tia \(DA\) sao cho \(DE = \frac{1}{4}AE.\)
a) \(\Delta ADC\) vuông tại \(D.\)
b) \(AD = \sqrt {135} \;{\rm{cm}}{\rm{.}}\)
c) \(EC = 5\;{\rm{cm}}{\rm{.}}\)
d) Chu vi \(\Delta DEC\) lớn hơn \(12\;{\rm{cm}}{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Cho \(\Delta ABC\) vuông tại \(A\) có chu vi bằng \(48\;{\rm{cm}}\) và \(\frac{{AB}}{{AC}} = \frac{3}{4}.\)
a) \(\frac{{BC}}{5} = \frac{{AB}}{4}.\)
b) \(\frac{{AB}}{4} = \frac{{AC}}{3} = \frac{{BC}}{5} = 2.\)
c) \(BC = 20\;{\rm{cm}}{\rm{.}}\)
d) Diện tích \(\Delta ABC\) bằng \(96\;{\rm{c}}{{\rm{m}}^{\rm{2}}}.\)
Cho \(\Delta ABC\) vuông tại \(A\) có chu vi bằng \(48\;{\rm{cm}}\) và \(\frac{{AB}}{{AC}} = \frac{3}{4}.\)
a) \(\frac{{BC}}{5} = \frac{{AB}}{4}.\)
b) \(\frac{{AB}}{4} = \frac{{AC}}{3} = \frac{{BC}}{5} = 2.\)
c) \(BC = 20\;{\rm{cm}}{\rm{.}}\)
d) Diện tích \(\Delta ABC\) bằng \(96\;{\rm{c}}{{\rm{m}}^{\rm{2}}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.