Cho \(\Delta ABC\) cân tại \(A\) có \(AB = 12\;{\rm{cm}}{\rm{, }}BC = 6\;{\rm{cm}}{\rm{.}}\) Gọi \(D\) là trung điểm của \(BC.\) Gọi \(E\) là điểm thuộc tia đối của tia \(DA\) sao cho \(DE = \frac{1}{4}AE.\)
a) \(\Delta ADC\) vuông tại \(D.\)
b) \(AD = \sqrt {135} \;{\rm{cm}}{\rm{.}}\)
c) \(EC = 5\;{\rm{cm}}{\rm{.}}\)
d) Chu vi \(\Delta DEC\) lớn hơn \(12\;{\rm{cm}}{\rm{.}}\)
Cho \(\Delta ABC\) cân tại \(A\) có \(AB = 12\;{\rm{cm}}{\rm{, }}BC = 6\;{\rm{cm}}{\rm{.}}\) Gọi \(D\) là trung điểm của \(BC.\) Gọi \(E\) là điểm thuộc tia đối của tia \(DA\) sao cho \(DE = \frac{1}{4}AE.\)
a) \(\Delta ADC\) vuông tại \(D.\)
b) \(AD = \sqrt {135} \;{\rm{cm}}{\rm{.}}\)
c) \(EC = 5\;{\rm{cm}}{\rm{.}}\)
d) Chu vi \(\Delta DEC\) lớn hơn \(12\;{\rm{cm}}{\rm{.}}\)
Quảng cáo
Trả lời:
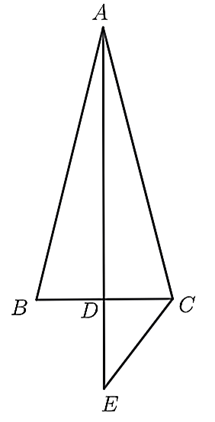
a) Đúng.
Vì \(\Delta ABC\) cân tại \(A\) nên \(AD\) là đường trung tuyến đồng thời là đường cao của \(\Delta ABC.\)
Do đó, \(AD \bot BC\) tại \(D.\) Suy ra, \(\Delta ADC\) vuông tại \(D.\)
b) Đúng.
Vì \(\Delta ABC\) cân tại \(A\) nên \(AC = AB = 12\;{\rm{cm}}.\) Ta có: \(DC = \frac{1}{2}BC = \frac{1}{2} \cdot 6 = 3\;\left( {{\rm{cm}}} \right).\)
Áp dụng định lí Pythagore vào \(\Delta ADC\) vuông tại \(D\) ta có:
\(A{D^2} + D{C^2} = A{C^2}\)
\(A{D^2} = A{C^2} - A{D^2} = {12^2} - {3^2} = 135\)
\(AD = \sqrt {135} \;{\rm{cm}}{\rm{.}}\)
Vậy \(AD = \sqrt {135} \;{\rm{cm}}{\rm{.}}\)
c) Sai.
Vì \(DE = \frac{1}{4}AE\) nên \(DE = \frac{1}{3}AD = \frac{{\sqrt {135} }}{3}\;{\rm{cm}}{\rm{.}}\)
Áp dụng định lí Pythagore vào \(\Delta EDC\) vuông tại \(D\) ta có:
\(E{C^2} = E{D^2} + D{C^2} = {\left( {\frac{{\sqrt {135} }}{3}} \right)^2} + {3^2} = 24\) nên \(EC = \sqrt {24} \;{\rm{cm}}{\rm{.}}\)
d) Sai.
Chu vi \(\Delta DEC\) là: \(P = EC + ED + DC = \sqrt {24} + \frac{{\sqrt {135} }}{3} + 3 \approx 11,8 < 12.\)
Vậy chu vi \(\Delta DEC\) nhỏ hơn \(12\;{\rm{cm}}{\rm{.}}\)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
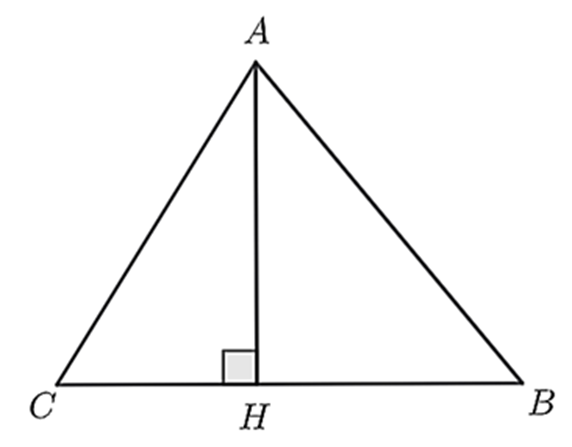
a) Đúng.
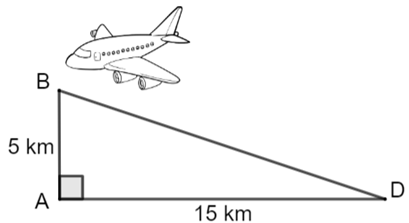
Vì \(AH\) là đường cao của \(\Delta ABC\) nên \(AH \bot BC.\) Do đó, \(\Delta ABH\) vuông tại \(H.\)
Nên \(A{H^2} + H{B^2} = A{B^2}\) (định lí Pythagore), suy ra \(A{H^2} = A{B^2} - H{B^2} = {\left( {\sqrt {80} } \right)^2} - {4^2} = 64.\)
Suy ra \(AH = \sqrt {64} = 8\;{\rm{m}}{\rm{.}}\) Vậy \(AH = 8\;{\rm{m}}{\rm{.}}\)
b) Sai.
Vì \(AH \bot BC\) nên \(\Delta ACH\) vuông tại \(H.\)
Suy ra \(A{H^2} + H{C^2} = A{C^2}\) (định lí Pythagore), suy ra \(C{H^2} = A{C^2} - A{H^2} = {10^2} - 64 = 36.\)
Suy ra \(CH = \sqrt {36} = 6\;{\rm{m}}{\rm{.}}\) Vậy \(CH = 6\;{\rm{m}}{\rm{.}}\)
c) Sai.
Chu vi \(\Delta AHC\) là: \({P_1} = AH + HC + AC = 8 + 6 + 10 = 24\;\left( {\rm{m}} \right).\)
Vậy chu vi \(\Delta AHC\) bằng \(24\;{\rm{m}}{\rm{.}}\)
d) Sai.
Ta có: \(BC = BH + CH = 4 + 6 = 10\;\left( {\rm{m}} \right).\)
Chu vi \(\Delta ABC\) là: \({P_2} = AC + AB + BC = 10 + \sqrt {80} + 10 = 20 + \sqrt {80} \;\left( {\rm{m}} \right).\)
Ta có: \({P_2} - {P_1} = 20 + \sqrt {80} - 24 = \sqrt {80} - 4 \approx 5\;\left( {\rm{m}} \right).\)
Vậy chu vi \(\Delta ABC\) lớn hơn chu vi \(\Delta AHC\) khoảng \(5\;{\rm{m}}{\rm{.}}\)
Lời giải
a) Sai.
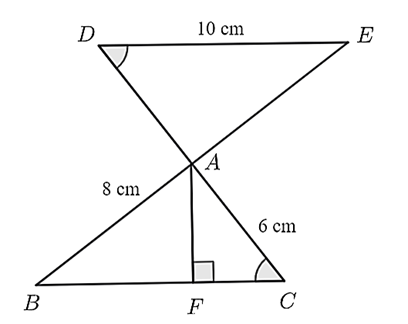
\(\Delta ADE\) và \(\Delta ACB\) có: \(\widehat D = \widehat C\;\left( {gt} \right),\;AD = AC\;\left( { = 6\;{\rm{cm}}} \right),\;\widehat {DAE} = \widehat {BAC}\) (hai góc đối đỉnh).
Do đó, \(\Delta ADE = \Delta ACB\;\left( {g - c - g} \right).\)
b) Đúng.
Vì \(\Delta ADE = \Delta ACB\;\left( {cmt} \right)\) nên \(DE = BC = 10\;{\rm{cm}}{\rm{.}}\)
Vì: \(A{B^2} + A{C^2} = B{C^2}\;\left( {{\rm{do}}\;{6^2} + {8^2} = {{10}^2}} \right)\) nên \(\Delta ABC\) vuông tại \(A\) (định lí Pythagore đảo).
c) Đúng.
Diện tích \(\Delta ABC\) vuông tại \(A\) là: \(S = \frac{1}{2}AB \cdot AC = \frac{1}{2} \cdot 6 \cdot 8 = 24\;\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
Vậy diện tích \(\Delta ABC\) bằng \(24\;{\rm{c}}{{\rm{m}}^2}.\)
d) Sai.
Vì \(AF\) là đường cao của \(\Delta ABC\) nên diện tích \(\Delta ABC\) là: \(S = \frac{1}{2}AF \cdot BC.\)
Suy ra: \(\frac{1}{2} \cdot AF \cdot 10 = 24,\) suy ra \(AF = 4,8\;{\rm{cm}}{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Cho \(\Delta ABC\) vuông tại \(A\) có chu vi bằng \(48\;{\rm{cm}}\) và \(\frac{{AB}}{{AC}} = \frac{3}{4}.\)
a) \(\frac{{BC}}{5} = \frac{{AB}}{4}.\)
b) \(\frac{{AB}}{4} = \frac{{AC}}{3} = \frac{{BC}}{5} = 2.\)
c) \(BC = 20\;{\rm{cm}}{\rm{.}}\)
d) Diện tích \(\Delta ABC\) bằng \(96\;{\rm{c}}{{\rm{m}}^{\rm{2}}}.\)
Cho \(\Delta ABC\) vuông tại \(A\) có chu vi bằng \(48\;{\rm{cm}}\) và \(\frac{{AB}}{{AC}} = \frac{3}{4}.\)
a) \(\frac{{BC}}{5} = \frac{{AB}}{4}.\)
b) \(\frac{{AB}}{4} = \frac{{AC}}{3} = \frac{{BC}}{5} = 2.\)
c) \(BC = 20\;{\rm{cm}}{\rm{.}}\)
d) Diện tích \(\Delta ABC\) bằng \(96\;{\rm{c}}{{\rm{m}}^{\rm{2}}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.