Cho tứ giác \(EFGH\) như hình vẽ:
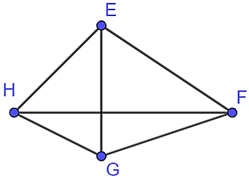
Cặp cạnh đối nhau là:
Cho tứ giác \(EFGH\) như hình vẽ:
Cặp cạnh đối nhau là:
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: D
Hai cạnh đối nhau của tứ giác \(EFGH\) là: \(HG\) và \(EF.\)Đang tải chế độ Học...
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(\widehat C = 50^\circ .\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: A
Tứ giác \(ABCD\) có: \[\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ .\]
Do đó, \[\widehat C = 360^\circ - \widehat A - \widehat B - \widehat D = 360^\circ - 80^\circ - 120^\circ - 110^\circ = 50^\circ .\] Vậy \[\widehat C = 50^\circ .\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
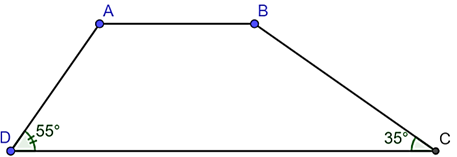
a) Sai.
Tứ giác \(ABCD\) có: \[\widehat {DAB} + \widehat {CBA} + \widehat {BCD} + \widehat {CDA} = 360^\circ \]
Suy ra \[\widehat {DAB} + \widehat {CBA} = 360^\circ - \widehat {BCD} - \widehat {CDA} = 360^\circ - 35^\circ - 55^\circ = 270^\circ .\]
Do đó, \(\widehat A + \widehat B = 270^\circ .\)
b) Đúng.
Vì \[\widehat {CBA} - \widehat {DAB} = 20^\circ \] nên \[\widehat {CBA} = \widehat {DAB} + 20^\circ .\]
Mà \[\widehat {DAB} + \widehat {CBA} = 270^\circ \] nên \[\widehat {DAB} + 20^\circ + \widehat {DAB} = 270^\circ ,\] suy ra \(2\widehat {DAB} = 250^\circ .\) Vậy \(\widehat {DAB} = 125^\circ .\)
c) Sai.
Vì \(\widehat {DAB} = 125^\circ \) nên \[\widehat {ABC} = \widehat {DAB} + 20^\circ = 125^\circ + 20^\circ = 145^\circ .\] Vậy \(\widehat B = 145^\circ .\)
d) Đúng.
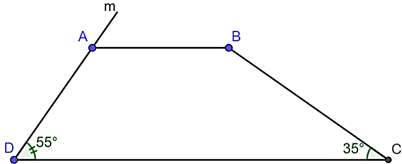
Kẻ \(Am\) là tia đối của tia \(AD.\)
Ta có: \(\widehat {DAB} + \widehat {BAm} = 180^\circ \) (hai góc kề bù) nên \(\widehat {BAm} = 180^\circ - \widehat {DAB} = 180^\circ - 125^\circ = 55^\circ .\)
Vì \(\widehat {BAm} = \widehat {ADC}\left( { = 55^\circ } \right),\) mà hai góc này ở vị trí đồng vị nên \(AB\,{\rm{//}}\,CD.\) Vậy \(AB\,{\rm{//}}\,CD.\)
Câu 3
A. \(\widehat A\) và \(\widehat C\) là hai góc đối nhau.
B. \(\widehat A\) và \(\widehat C\) là hai góc kề nhau.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập