Bác An có một khu vườn, bác chia khu vườn thành hai phần như hình vẽ:

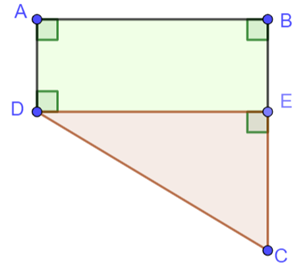
$Phần màu nâu dùng để trồng rau có diện tích là $30\;{{\rm{m}}^2}.$ Phần màu xanh dùng để trồng cây ăn quả. Biết rằng $AD = 4\;{\rm{m}},\;BC = 10\;{\rm{m}}.$ Hỏi độ dài $AB$ bằng bao nhiêu mét? (ảnh 1)$

Phần màu nâu dùng để trồng rau có diện tích là $30\;{{\rm{m}}^2}.$ Phần màu xanh dùng để trồng cây ăn quả.

Biết rằng $AD = 4\;{\rm{m}},\;BC = 10\;{\rm{m}}.$ Hỏi độ dài $AB$ bằng bao nhiêu mét?

Xem lời giải

Câu hỏi trong đề: 20 câu trắc nghiệm Toán 8 Cánh diều Bài 18. Hình chữ nhật (Đúng sai - Trả lời ngắn) có đáp án !!

Bắt đầu thi

Quảng cáo

Trả lời:

Giải bởi Vietjack

Đáp án: $10$

Tứ giác $ABED$ có: $\widehat A = \widehat B = \widehat {BED} = \widehat {EDA} = 90^\circ $ nên tứ giác $ABED$ là hình chữ nhật.

Do đó, $EB = AD = 4\;{\rm{m}}{\rm{,}}\;AB = DE.$

Ta có: $EC = CB - BE = 10 - 4 = 6\;\left( {\rm{m}} \right).$

Diện tích tam giác $DEC$ vuông tại $E$ bằng $30\;{{\rm{m}}^2}$ nên $\frac{1}{2} \cdot EC \cdot DE = 30$.

Suy ra $\frac{1}{2} \cdot 6 \cdot DE = 30$, do đó $DE = 10\;{\rm{m}}.$

Do đó, $AB = DE = 10\;{\rm{m}}.$ Vậy $AB = 10\;{\rm{m}}.$

Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay

Sách thầy cô Vietjack biên soạn:

Xem thêm »

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1

Cho hình chữ nhật $ABCD$ có chu vi bằng $14\;{\rm{cm}}{\rm{.}}$ Biết rằng chu vi tam giác $ACD$ bằng $12\;{\rm{cm}}{\rm{.}}$ Tính độ dài đường chéo $BD.$ (Đơn vị: cm).

Xem đáp án

Lời giải

Đáp án: $5$

Vì chu vi hình chữ nhật $ABCD$ bằng $14\;{\rm{cm}}$ nên $2\left( {DC + AD} \right) = 14\;{\rm{cm}}$ nên $AD + DC = 7\;{\rm{cm}}{\rm{.}}$

Vì chu vi tam giác $ACD$ bằng $12\;{\rm{cm}}$ nên $DC + AD + AC = 12\;\left( {{\rm{cm}}} \right).$

Do đó, $7 + AC = 12$ hay $AC = 5\;{\rm{cm}}{\rm{.}}$

Vì tứ giác $ABCD$ là hình chữ nhật nên $BD = AC = 5\;{\rm{cm}}{\rm{.}}$ Vậy $BD = 5\;{\rm{cm}}{\rm{.}}$

Câu 2

Cho hình chữ nhật $ABCD$ hai đường chéo cắt nhau tại $O.$ Gọi $M,\;N$ lần lượt là trung điểm của $AB,\;BC.$

         a) $\widehat {OMB} = \widehat {ONB} = 90^\circ .$

         b) Tứ giác $OMBN$ là hình chữ nhật.

         c) $MN = \frac{1}{3}AC.$

         d) $MN\,{\rm{//}}\,AC.$

Xem đáp án

Lời giải

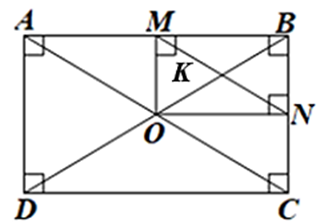
$Cho hình chữ nhật $ABCD$ hai đường chéo cắt nhau tại $O.$ Gọi $M,\;N$ lần lượt là trung điểm của $AB,\;BC.$ a) $\widehat {OMB} = \widehat {ONB} = 90^\circ .$ (ảnh 1)$

a) Đúng.

Tứ giác $ABCD$ là hình chữ nhật nên $OA = OB = OC = OD = \frac{1}{2}AC = \frac{1}{2}BD.$

Do đó, tam giác $AOB$ cân tại $O$ và tam giác $COB$ cân tại $O.$

Tam giác $AOB$ cân tại $O$ nên $OM$ là đường trung tuyến đồng thời là đường cao của tam giác đó. Do đó, $\widehat {OMB} = 90^\circ .$

Tam giác $COB$ cân tại $O$ nên $ON$ là đường trung tuyến đồng thời là đường cao của tam giác đó. Do đó, $\widehat {ONB} = 90^\circ .$

b) Đúng.

Tứ giác $OMBN$ có: $\widehat {MBN} = \widehat {OMB} = \widehat {ONB} = 90^\circ .$ Do đó, tứ giác $OMBN$ là hình chữ nhật.

c) Sai.

Vì tứ giác $OMBN$ là hình chữ nhật nên $MN = OB.$ Mà $OB = \frac{1}{2}AC$ nên $MN = \frac{1}{2}AC.$

d) Đúng.

Gọi $K$ là giao điểm của $OB$ và $MN.$ Vì tứ giác $OMBN$ là hình chữ nhật nên $KM = KB.$

Do đó, tam giác $KMB$ cân tại $K.$ Do đó, $\widehat {KMB} = \widehat {KBM}.$

Vì tam giác $AOB$ cân tại $O$ nên $\widehat {OAB} = \widehat {OBA}.$ Do đó, $\widehat {OAB} = \widehat {KMB}.$

Mà hai góc này ở vị trí đồng vị nên $MN\,{\rm{//}}\,AC.$

Câu 3