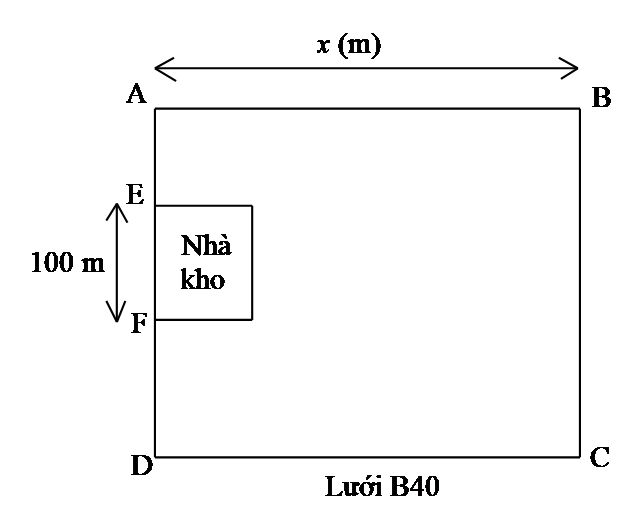Cho tam giác \(ABC\) vuông tại \(A,\) đường trung tuyến \(AM.\) Gọi \(D\) là trung điểm của \(AB.\) Trên tia đối của tia \(DM\) lấy điểm \(E\) sao cho \(DE = DM.\)
a) Các tứ giác \(AEBM\) và \(ACME\) là hình gì? Tại sao?
b) Tam giác vuông \(ABC\) có điều kiện gì thì \(AEBM\) là hình vuông?
Cho tam giác \(ABC\) vuông tại \(A,\) đường trung tuyến \(AM.\) Gọi \(D\) là trung điểm của \(AB.\) Trên tia đối của tia \(DM\) lấy điểm \(E\) sao cho \(DE = DM.\)
a) Các tứ giác \(AEBM\) và \(ACME\) là hình gì? Tại sao?
b) Tam giác vuông \(ABC\) có điều kiện gì thì \(AEBM\) là hình vuông?
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) ⦁ Ta có \(DE = DM\) nên \(D\) là trung điểm của \(EM.\)
Xét tứ giác \(AEBM\) có \(D\) là trung điểm của hai đường chéo \(AB\) và \(EM\) nên tứ giác \(AEBM\) là hình bình hành (dấu hiệu nhận biết).
Xét \(\Delta ABC\) vuông tại \(A\) có đường trung tuyến \(AM\) ứng với cạnh huyền \(BC\) nên \(AM = \frac{1}{2}BC\) (tính chất đường trung tuyến ứng với cạnh huyền).Vì \(AM\) là đường trung tuyến nên \(M\) là trung điểm của \(BC,\) do đó \(BM = CM = \frac{1}{2}BC.\)
Suy ra \(AM = BM = CM.\)
Hình bình hành \(AEBM\) có hai cạnh kề bằng nhau \(AM = BM\) nên là hình thoi.
⦁ Do \(AEBM\) hình thoi nên \(AE = BM\) và \(AE\,{\rm{//}}\,BM.\)
Do đó \(AE = CM\,\,\left( { = BM} \right)\) và \(AE\,{\rm{//}}\,CM.\)
Tứ giác \(ACME\) có \(AE = CM\) và \(AE\,{\rm{//}}\,CM\) nên là hình bình hành (dấu hiệu nhận biết).
b) Do\(AEBM\) là hình thoi nên để \(AEBM\) là hình vuông thì \(\widehat {AMB} = 90^\circ \) hay \(AM \bot BC\)
Khi đó \(\Delta ABC\) có đường trung tuyến \(AM\) đồng thời là đường cao nên sẽ là tam giác cân tại \(A.\)
Vậy \(\Delta ABC\) vuông cân tại \(A\) thì \(AEBM\) là hình vuông.
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
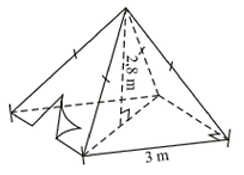
a) Diện tích đáy hình vuông của chiếc lều là:
Thể tích không khí bên trong chiếc lều là:
b) Diện tích xung quanh của chiếc lều là:
\({S_{xq}} = \frac{1}{2} \cdot C \cdot d = \frac{1}{2} \cdot \left( {4 \cdot 3} \right) \cdot 3,18 = 19,08{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Diện tích vải phủ bốn phía và trải nền đất cho chiếc lều là:
\(S = 9 + 19,08 = 28,08\) (m2).
Do \(28,08 > 20\) nên số tiền mua vải được giảm giá \(5\% \) trên tổng hóa đơn.
Vậy số tiền mua vải là: \(28,08 \cdot 15\,\,000 \cdot \left( {100\% - 5\% } \right) = 400\,\,140\) (đồng).
Lời giải
![Tứ giác \[ADHE\] là hình gì? Vì sao? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/26-1758293616.png)
a) Vì \(\Delta ABC\) vuông tại \(A\) nên \(\widehat {BAC} = 90^\circ \) hay \(\widehat {DAE} = 90^\circ \).
Ta có \(HD \bot AB\); \(HE \bot AC\) nên \(\widehat {HDA} = 90^\circ \); \(\widehat {HEA} = 90^\circ \).
Tứ giác \(ADHE\) có \[\widehat {DAE} = \widehat {HDA} = \widehat {HEA} = 90^\circ \] nên tứ giác \(ADHE\) là hình chữ nhật.
b) Xét \(\Delta AHD\) vuông tại \(D\), áp dụng định lý Pythagore, ta có: \(A{H^2} = A{D^2} + D{H^2}\)
Suy ra \(D{H^2} = A{H^2} - A{D^2} = {5^2} - {4^2} = 9\). Do đó \(DH = 3\,\,\left( {{\rm{cm}}} \right){\rm{.}}\)
Tứ giác \(ADHE\) là hình chữ nhật nên ta có: \({S_{ADHE}} = AD\,.\,DH = 4\,.\,3 = 12\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\).
Vậy diện tích tứ giác \(ADHE\) bằng \(12\,\,{\rm{c}}{{\rm{m}}^{\rm{2}}}.\)
c) Xét tứ giác \(BKIH\) có \(D\) là trung điểm của hai đường chéo \(BI\) và \(HK\) nên \(BKIH\) là hình bình hành (dấu hiệu nhận biết).
Do đó \(KI\,{\rm{//}}\,BH.\)
Mà \(AH \bot BH\) suy ra \(KI \bot AH.\)
Xét \(\Delta AHK\) có hai đường cao \(AD,\,\,KI\) \(\left( {AD \bot KH;\,\,KI \bot AH} \right)\) cắt nhau tại \(I\) nên \(I\) là trực tâm của tam giác \(AKH\), suy ra \(HI \bot AK.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo