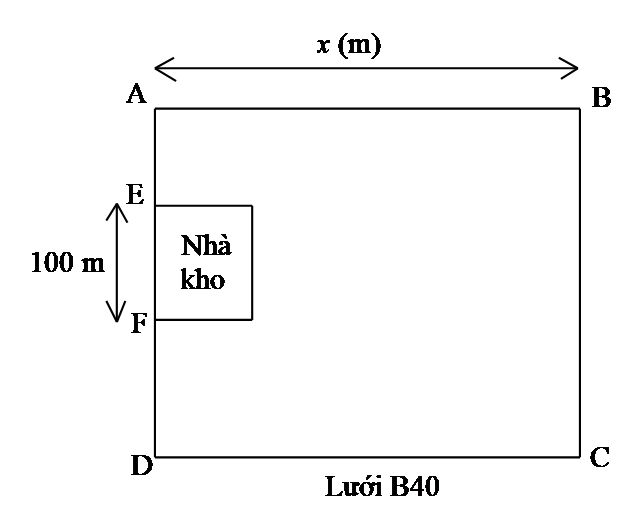Chứng minh rằng
a) Nếu \[x\] là số tự nhiên không chia hết cho \[3\] thì \(M = 2{x^2} - 5\) chia hết cho \[3\] .
b) Nếu \(x\) là số tự nhiên lẻ thì \(N = {x^3} + 3{x^2} - x - 3\) chia hết cho \[8\] .
c) Đa thức \[M = x\left( {x + 1} \right)\left( {x + 2} \right)\left( {x + 3} \right) + 1\] (với \(x \in \mathbb{Z}\)) là bình phương của một số nguyên.
Chứng minh rằng
a) Nếu \[x\] là số tự nhiên không chia hết cho \[3\] thì \(M = 2{x^2} - 5\) chia hết cho \[3\] .
b) Nếu \(x\) là số tự nhiên lẻ thì \(N = {x^3} + 3{x^2} - x - 3\) chia hết cho \[8\] .
c) Đa thức \[M = x\left( {x + 1} \right)\left( {x + 2} \right)\left( {x + 3} \right) + 1\] (với \(x \in \mathbb{Z}\)) là bình phương của một số nguyên.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
a) Vì \[x\] là số tự nhiên không chia hết cho \[3\] nên ta có \(x = 3k + 1\) hoặc \(x = 3k + 2\,\,\left( {k \in \mathbb{N}} \right)\).
⦁ Với \(x = 3k + 1\) ta có: \[M = 2{\left( {3k + 1} \right)^2} - 5\]\[ = 2\left( {9{k^2} + 6k + 1} \right) - 5\]
\[ = 18{k^2} + 12k + 2 - 5\]\[ = 18{k^2} + 12k - 3 = 3\left( {6{k^2} + 4k - 1} \right)\,\, \vdots \,\,3\].
⦁ Với \(x = 3k + 2\) ta có: \[M = 2{\left( {3k + 2} \right)^2} - 5\]\[ = 2\left( {9{k^2} + 12k + 4} \right) - 5\]
\[ = 18{k^2} + 24k + 8 - 5\]\[ = 18{k^2} + 24k + 3\]\[ = 3\left( {6{k^2} + 8k + 1} \right)\,\, \vdots \,\,3\].
Vậy \[x\] là số tự nhiên không chia hết cho \[3\] thì \(M = 2{x^2} - 5\) chia hết cho \[3\].
b) Vì \(x\) là số tự nhiên lẻ nên ta có \(x = 2k + 1\,\,\left( {k \in \mathbb{N}} \right)\). Do đó:
\(N = {\left( {2k + 1} \right)^3} + 3{\left( {2k + 1} \right)^2} - \left( {2k + 1} \right) - 3\)
\( = 8{k^3} + 12{k^2} + 6k + 1 + 12{k^2} + 12k + 3 - 2k - 1 - 3\)
\( = 8{k^3} + 24{k^2} + 16k\)
\( = 8\left( {{k^3} + 3{k^2} + 2k} \right)\,\, \vdots \,\,8\)
Vậy \(x\) là số tự nhiên lẻ thì \(N = {x^3} + 3{x^2} - x - 3\) chia hết cho \[8\].
c) Ta có \[M = x\left( {x + 1} \right)\left( {x + 2} \right)\left( {x + 3} \right) + 1\]\( = x\left( {x + 3} \right)\left( {x + 2} \right)\left( {x + 1} \right) + 1\)
\( = \left( {{x^2} + 3x} \right)\left( {{x^2} + 3x + 2} \right) + 1\)\( = {\left( {{x^2} + 3x} \right)^2} + 2\left( {{x^2} + 3x} \right) + 1\)\( = {\left( {{x^2} + 3x + 1} \right)^2}\).
Với \(x \in \mathbb{Z}\) ta có \(\left( {{x^2} + 3x + 1} \right) \in \mathbb{Z}\). Do đó \({\left( {{x^2} + 3x + 1} \right)^2}\) là bình phương của một số nguyên.
Vậy đa thức \[M = x\left( {x + 1} \right)\left( {x + 2} \right)\left( {x + 3} \right) + 1\] (với \(x \in \mathbb{Z}\)) là bình phương của một số nguyên.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
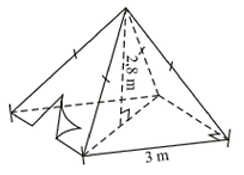
a) Diện tích đáy hình vuông của chiếc lều là:
Thể tích không khí bên trong chiếc lều là:
b) Diện tích xung quanh của chiếc lều là:
\({S_{xq}} = \frac{1}{2} \cdot C \cdot d = \frac{1}{2} \cdot \left( {4 \cdot 3} \right) \cdot 3,18 = 19,08{\rm{\;(}}{{\rm{m}}^2}{\rm{)}}{\rm{.}}\)
Diện tích vải phủ bốn phía và trải nền đất cho chiếc lều là:
\(S = 9 + 19,08 = 28,08\) (m2).
Do \(28,08 > 20\) nên số tiền mua vải được giảm giá \(5\% \) trên tổng hóa đơn.
Vậy số tiền mua vải là: \(28,08 \cdot 15\,\,000 \cdot \left( {100\% - 5\% } \right) = 400\,\,140\) (đồng).
Lời giải
Hướng dẫn giải
Vì tấm lưới dài \(500\,\,{\rm{m}}\), hay chính là chu vi của mảnh vườn hình chữ nhật \(ABCD\) trừ khu nhà kho \[EF = 100\,\,{\rm{m}}\] bằng \(500\,\,{\rm{m}}\).
Suy ra chu vi của mảnh vườn là \(600\,\,{\rm{m}}\), nên nửa chu vi mảnh vườn là \(300{\rm{\;m}}.\)
Do đó chiều rộng của mảnh vườn rào được theo chiều dài \(x{\rm{\;(m)}}\) là: \(300 - x{\rm{\;(m)}}{\rm{.}}\)
Diện tích mảnh vườn hình chữ nhật là:
\[S = x \cdot \left( {300 - x} \right)\]\( = - {x^2} + 300x\)
\( = - {x^2} + 2 \cdot x \cdot 150 - {150^2} + {150^2}\)
\( = - {\left( {x - 150} \right)^2} + 22\,\,500\)
Với mọi \(x > 0,\) ta có \({\left( {x - 150} \right)^2} \ge 0\) nên \( - {\left( {x - 150} \right)^2} \le 0\) hay \( - {\left( {x - 150} \right)^2} + 22\,\,500 \le 22\,\,500\).
Dấu “=” xảy ra khi \(x = 150\).
Vậy diện tích mảnh vườn lớn nhất là \(22\,\,500{\rm{\;}}{{\rm{m}}^2}\) khi \(x = 150{\rm{\;m}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập