Cho tam giác \(ABC\) vuông tại \(A,\) đường trung tuyến \(AM.\) Gọi \(D\) là trung điểm của \(AB.\) Trên tia đối của tia \(DM\) lấy điểm \(E\) sao cho \(DE = DM.\)
a) Các tứ giác \(AEBM\) và \(ACME\) là hình gì? Tại sao?
b) Tam giác vuông \(ABC\) có điều kiện gì thì \(AEBM\) là hình vuông?
Cho tam giác \(ABC\) vuông tại \(A,\) đường trung tuyến \(AM.\) Gọi \(D\) là trung điểm của \(AB.\) Trên tia đối của tia \(DM\) lấy điểm \(E\) sao cho \(DE = DM.\)
a) Các tứ giác \(AEBM\) và \(ACME\) là hình gì? Tại sao?
b) Tam giác vuông \(ABC\) có điều kiện gì thì \(AEBM\) là hình vuông?
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) ⦁ Ta có \(DE = DM\) nên \(D\) là trung điểm của \(EM.\)
Xét tứ giác \(AEBM\) có \(D\) là trung điểm của hai đường chéo \(AB\) và \(EM\) nên tứ giác \(AEBM\) là hình bình hành (dấu hiệu nhận biết).
Xét \(\Delta ABC\) vuông tại \(A\) có đường trung tuyến \(AM\) ứng với cạnh huyền \(BC\) nên \(AM = \frac{1}{2}BC\) (tính chất đường trung tuyến ứng với cạnh huyền).Vì \(AM\) là đường trung tuyến nên \(M\) là trung điểm của \(BC,\) do đó \(BM = CM = \frac{1}{2}BC.\)
Suy ra \(AM = BM = CM.\)
Hình bình hành \(AEBM\) có hai cạnh kề bằng nhau \(AM = BM\) nên là hình thoi.
⦁ Do \(AEBM\) hình thoi nên \(AE = BM\) và \(AE\,{\rm{//}}\,BM.\)
Do đó \(AE = CM\,\,\left( { = BM} \right)\) và \(AE\,{\rm{//}}\,CM.\)
Tứ giác \(ACME\) có \(AE = CM\) và \(AE\,{\rm{//}}\,CM\) nên là hình bình hành (dấu hiệu nhận biết).
b) Do\(AEBM\) là hình thoi nên để \(AEBM\) là hình vuông thì \(\widehat {AMB} = 90^\circ \) hay \(AM \bot BC\)
Khi đó \(\Delta ABC\) có đường trung tuyến \(AM\) đồng thời là đường cao nên sẽ là tam giác cân tại \(A.\)
Vậy \(\Delta ABC\) vuông cân tại \(A\) thì \(AEBM\) là hình vuông.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
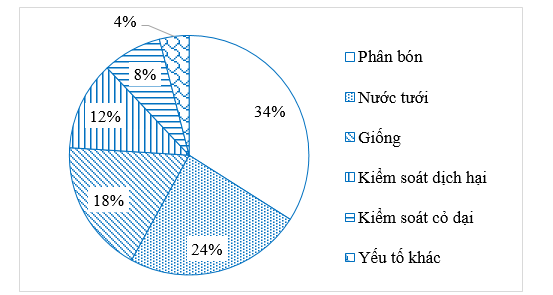
a) Yếu tố Phân bón (chiếm \(34\% )\) ảnh hưởng đến sinh trưởng của cây trồng nhiều nhất.
b) Trong các yếu tố ảnh hưởng đến sinh trưởng của cây thì Yếu tố kiểm soát dịch hại gấp số lần Yếu tố khác là: \(\frac{{12\% }}{{4\% }} = 3\) (lần).
c) Một vài biện pháp khắc phục tình trạng vấn đề tưới nước để làm giảm thiệt hại trong việc trồng trọt: khoan thêm giếng, lắp đặt thêm ống dẫn nước từ các hồ chứa, xây dựng phương án tưới cho phù hợp với từng loại cây trồng, áp dụng phương pháp tưới tiết kiệm nước theo hình thức khô – nước xen kẽ, chỉ vô nước giai đoạn bón phân.
Lời giải
Hướng dẫn giải
b) Ta có: \(B = \frac{{{x^{24}} + {x^{20}} + {x^{16}} + ... + {x^4} + 1}}{{{x^{26}} + {x^{24}} + {x^{22}} + ... + {x^2} + 1}},\) xét phân thức nghịch đảo của phân thức \(B\) là:
\(\frac{1}{B} = \frac{{{x^{26}} + {x^{24}} + {x^{22}} + ... + {x^2} + 1}}{{{x^{24}} + {x^{20}} + {x^{16}} + ... + {x^4} + 1}}\)
\( = \frac{{\left( {{x^{26}} + {x^{22}} + {x^{18}} + ... + {x^6} + {x^2}} \right) + \left( {{x^{24}} + {x^{20}} + ... + {x^4} + 1} \right)}}{{{x^{24}} + {x^{20}} + {x^{16}} + ... + {x^4} + 1}}\)
\( = \frac{{{x^2}\left( {{x^{24}} + {x^{20}} + ... + {x^4} + 1} \right) + \left( {{x^{24}} + {x^{20}} + ... + {x^4} + 1} \right)}}{{{x^{24}} + {x^{20}} + {x^{16}} + ... + {x^4} + 1}}\)
\( = \frac{{\left( {{x^{24}} + {x^{20}} + ... + 1} \right)\left( {{x^2} + 1} \right)}}{{{x^{24}} + {x^{20}} + {x^{16}} + ... + {x^4} + 1}} = {x^2} + 1.\)
Vậy \(B = \frac{1}{{{x^2} + 1}}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập