Hình ảnh bên là khối rubik có bốn mặt , các mặt bên, mặt đáy là các tam giác đều.
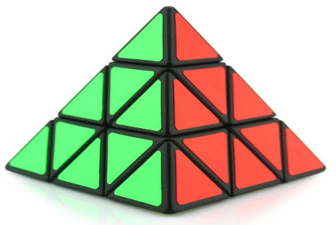
a) Khối rubik có dạng như hình bên thường được gọi là hình gì?
b) Cho biết số mặt, số cạnh, số đỉnh của hình khối bên ?
c) Hình vẽ bên là hình ảnh một chiếc rubik – 4 mặt , mỗi mặt đều được ghép bởi những tam giác đều nhỏ bằng nhau. Hãy cho biết có bao nhiêu tam giác đều có trên một mặt của chiếc rubik này?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
a) Khối rubik có dạng như hình bên thường được gọi là hình chóp tam giác đều.
b) Số mặt là 4; số cạnh là 6; số đỉnh là 1.
c) Có 13 tam giác đều có trên một mặt của chiếc rubik này.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
a) Thể tích kim tự tháp là: \[V = \frac{1}{3}.\,{34^2}.\,21 = 8\,\,092\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\].
b) Diện tích một viên gạch hình vuông là: \[S = {\left( {0,6} \right)^2} = 0,36\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\]
Số viên gạch hình vuông cần dùng là: \(\frac{{1\,\,000}}{{0,36}} \approx 2\,\,778\) (viên)
c) Số tấm kính hình thoi trên mỗi mặt là: \(\frac{{17\,.\,\left( {17 + 1} \right)}}{2} = 153\) (tấm)
Vậy có 153 tấm kính hình thoi trên mỗi mặt.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Ta có \({x^2} + {y^2} - 3x - 3y + xy + 3 = 0\)
\(2{x^2} + 2{y^2} - 6x - 6y + 2xy + 6 = 0\)
\({\left( {x + y - 2} \right)^2} + {\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 0\).
Từ đó suy ra \[x = y = 1.\]
Thay \(x = y = 1\) vào biểu thức Q ta được \(Q = {\left( {1 - 1} \right)^{2023}} + {\left( {1 - 2} \right)^{2024}} + {1^{2025}} = 0 + 1 + 1 = 2\).
Vậy \[Q = 2.\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập