Người ta buộc chú cún bằng sợi dây có một đầu buộc cố định tại điểm \(O\) làm cho chú cún cách điểm \(O\) xa nhất là \(9{\rm{\;m}}.\) Hỏi với các kích thước đã cho như hình trên, chú cún có thể đến các vị trí \(A,\,\,B,\,\,C,\,\,D\) để canh giữ mảnh vườn hình chữ nhật \[ABCD\] hay không?
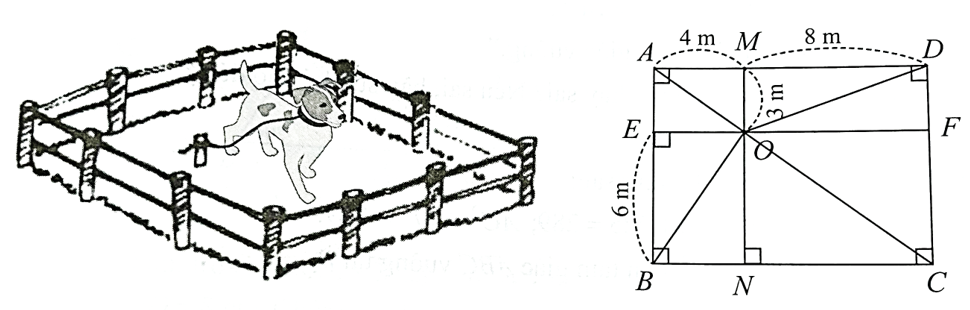
Người ta buộc chú cún bằng sợi dây có một đầu buộc cố định tại điểm \(O\) làm cho chú cún cách điểm \(O\) xa nhất là \(9{\rm{\;m}}.\) Hỏi với các kích thước đã cho như hình trên, chú cún có thể đến các vị trí \(A,\,\,B,\,\,C,\,\,D\) để canh giữ mảnh vườn hình chữ nhật \[ABCD\] hay không?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Áp dụng định lí Pythagore cho các tam giác vuông \(AMO,\,\,ONC,\,\,OMD,\,\,OBE,\) ta tính được:
⦁ \(O{A^2} = {3^2} + {4^2} = 25\) hay \(OA = 5{\rm{\;m;}}\)
⦁ \(O{C^2} = {6^2} + {8^2} = 100\) hay \(OC = 10{\rm{\;m}};\)
⦁ \(O{D^2} = {3^2} + {8^2} = 73\) hay \(OD = \sqrt {73} {\rm{\;m}};\)
⦁ \(O{B^2} = {4^2} + {6^2} = 52\) hay \(OB = \sqrt {52} {\rm{\;m}}{\rm{.}}\)
Ta thấy \[OA = 5{\rm{\;m}} < 9{\rm{\;m}},\,\,OD = \sqrt {73} {\rm{\;m}} < 9{\rm{\;m}},\,\,OB = \sqrt {52} {\rm{\;m}} < 9{\rm{\;m}},\,\,OC = 10{\rm{\;m}} > 9{\rm{\;m}}\,{\rm{.}}\]
Do đó, chú cún có thể đến các vị trí \(A,\,\,D,\,\,B\) nhưng không thể đến được vị trí \(C.\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
a) Thể tích kim tự tháp là: \[V = \frac{1}{3}.\,{34^2}.\,21 = 8\,\,092\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\].
b) Diện tích một viên gạch hình vuông là: \[S = {\left( {0,6} \right)^2} = 0,36\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\]
Số viên gạch hình vuông cần dùng là: \(\frac{{1\,\,000}}{{0,36}} \approx 2\,\,778\) (viên)
c) Số tấm kính hình thoi trên mỗi mặt là: \(\frac{{17\,.\,\left( {17 + 1} \right)}}{2} = 153\) (tấm)
Vậy có 153 tấm kính hình thoi trên mỗi mặt.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Ta có \({x^2} + {y^2} - 3x - 3y + xy + 3 = 0\)
\(2{x^2} + 2{y^2} - 6x - 6y + 2xy + 6 = 0\)
\({\left( {x + y - 2} \right)^2} + {\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 0\).
Từ đó suy ra \[x = y = 1.\]
Thay \(x = y = 1\) vào biểu thức Q ta được \(Q = {\left( {1 - 1} \right)^{2023}} + {\left( {1 - 2} \right)^{2024}} + {1^{2025}} = 0 + 1 + 1 = 2\).
Vậy \[Q = 2.\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập