Khu vườn của nhà bác Hoa có dạng hình vuông. Bác Hoa muốn dành một mảnh đất có dạng hình chữ nhật ở góc khu vườn làm nhà để dụng cụ làm vườn (hình vẽ).
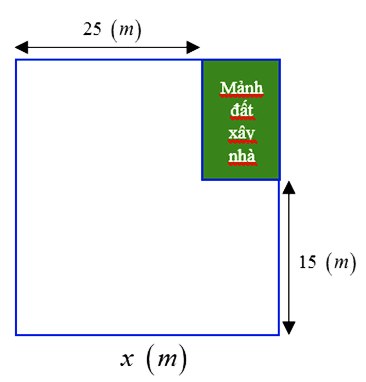
a) Viết đa thức biểu thị chu vi của mảnh đất làm nhà.
b) Biết chu vi của mảnh đất dành để làm nhà bằng \[40\,\,{\rm{m}}\]. Tính diện tích của khu vườn hình vuông ban đầu.
Khu vườn của nhà bác Hoa có dạng hình vuông. Bác Hoa muốn dành một mảnh đất có dạng hình chữ nhật ở góc khu vườn làm nhà để dụng cụ làm vườn (hình vẽ).

a) Viết đa thức biểu thị chu vi của mảnh đất làm nhà.
b) Biết chu vi của mảnh đất dành để làm nhà bằng \[40\,\,{\rm{m}}\]. Tính diện tích của khu vườn hình vuông ban đầu.
Quảng cáo
Trả lời:
a) Chu vi mảnh đất làm nhà là: \(2\left( {x - 25 + x - 15} \right) = 2\left( {2x - 40} \right) = 4x - 80\).
Vậy đa thức biểu thị chu vi của mảnh đất làm nhà \(4x - 80\) (m).
b) Vì chu vi của mảnh đất dành để làm nhà bằng \[40\,\,{\rm{m}}\] nên ta có
\(4x - 80 = 40\) hay \(4x = 120\) nên \(x = 30\).
Diện tích của khu vườn hình vuông ban đầu là \[{30^2} = 900{\rm{ }}({{\rm{m}}^{\rm{2}}}).\]
Vậy diện tích của khu vườn hình vuông ban đầu là \[900{\rm{ }}{{\rm{m}}^{\rm{2}}}.\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Ta có \({x^2} + {y^2} - 3x - 3y + xy + 3 = 0\)
\(2{x^2} + 2{y^2} - 6x - 6y + 2xy + 6 = 0\)
\({\left( {x + y - 2} \right)^2} + {\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 0\).
Từ đó suy ra \[x = y = 1.\]
Thay \(x = y = 1\) vào biểu thức Q ta được \(Q = {\left( {1 - 1} \right)^{2023}} + {\left( {1 - 2} \right)^{2024}} + {1^{2025}} = 0 + 1 + 1 = 2\).
Vậy \[Q = 2.\]
Lời giải
Hướng dẫn giải
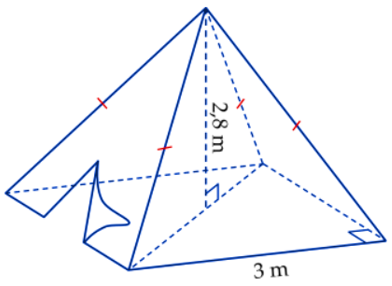
a) Thể tích kim tự tháp là: \[V = \frac{1}{3}.\,{34^2}.\,21 = 8\,\,092\,\,\left( {{{\rm{m}}^{\rm{3}}}} \right)\].
b) Diện tích một viên gạch hình vuông là: \[S = {\left( {0,6} \right)^2} = 0,36\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\]
Số viên gạch hình vuông cần dùng là: \(\frac{{1\,\,000}}{{0,36}} \approx 2\,\,778\) (viên)
c) Số tấm kính hình thoi trên mỗi mặt là: \(\frac{{17\,.\,\left( {17 + 1} \right)}}{2} = 153\) (tấm)
Vậy có 153 tấm kính hình thoi trên mỗi mặt.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.