Trên một công trường xây dựng, do cải tiến kỹ thuật nên năng suất lao động của công nhân tăng \(25\% \). Hỏi nếu số công nhân không thay đổi thì thời gian làm xong việc giảm bao nhiêu phần trăm?

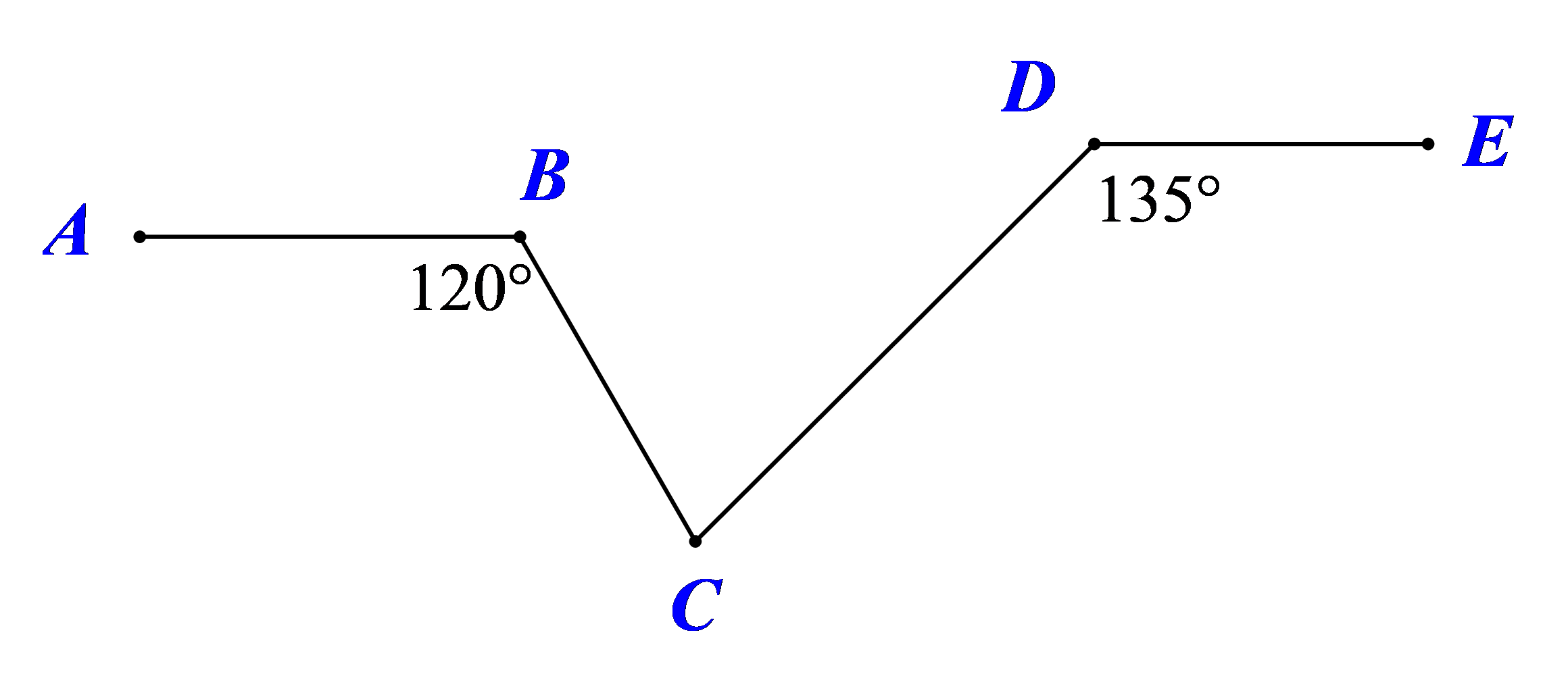
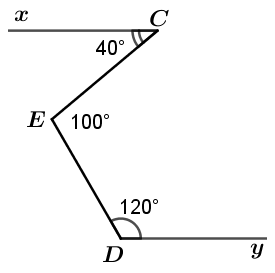
Kẻ đường thẳng qua \(C\) và song song với \[AB\].

Mà \(AB\,{\rm{//}}\,DE\) nên đường thẳng đó cũng song song với \[DE\].

Do đó \({\widehat C_1} + \widehat {ABC} = 180^\circ \) và \(\widehat {{C_2}} + \widehat {CDE} = 180^\circ \) (hai góc trong cùng phía)

Do đó, \[{\widehat C_1} = 60^\circ \] và \[\,{\widehat C_2} = 45^\circ \].

Suy ra \[\widehat {BCD} = 180^\circ - 60^\circ - 45^\circ = 75^\circ \].

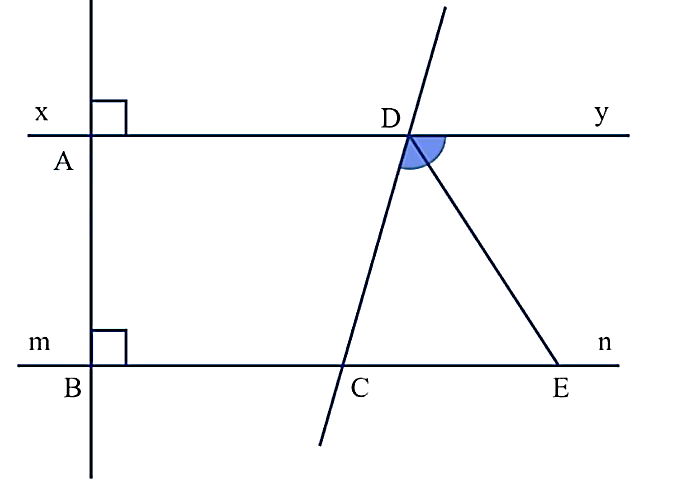
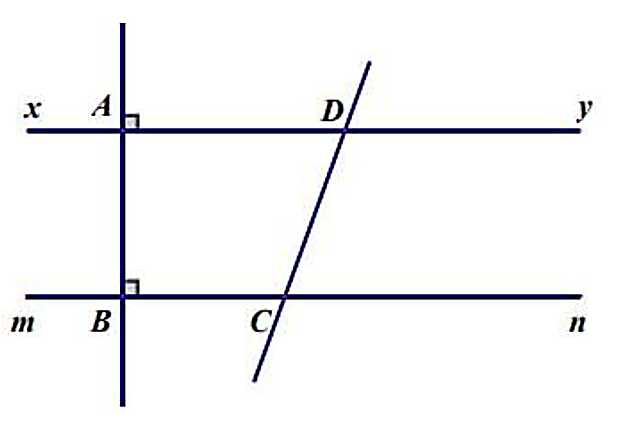
a) Ta có: \(xy \bot AB\) và \(mn \bot AB\) nên \(xy\parallel mn.\)

b) Ta có: \(\widehat {DCB} + \widehat {DCn} = 180^\circ \) (hai góc kề bù).

Suy ra \(\widehat {DCB} = 180^\circ - \widehat {DCn} = 180^\circ - 70^\circ = 110^\circ \).

Vì \(xy\parallel mn\) suy ra \(\widehat {DCB} = \widehat {CDy} = 110^\circ \) (hai góc so le trong).

c) Vì \(DE\) là tia phân giác của \(\widehat {CDy}\) nên \(\widehat {CDE} = \widehat {EDy} = \frac{{\widehat {CDy}}}{2} = \frac{{110^\circ }}{2} = 55^\circ \).

Vì \(xy\parallel mn\) suy ra \(\widehat {ECD} = \widehat {ADC} = 70^\circ \) (hai góc so le trong)

Mà \(\widehat {ADE} = \widehat {ADC} + \widehat {CDE} = 70^\circ + 55^\circ = 125^\circ \).