Ban tổ chức có 40 phần quà đem phát cho 13 đội. Có \[x\] đội vì công việc nên phải rời đi sớm, mỗi đội nhận được 3 phần quà và không tham gia vào lần phát quà. Phần quà còn lại được chia đều cho các đội còn lại. Hỏi mỗi đội còn lại nhận được nhiều nhất bao nhiêu phần quà?

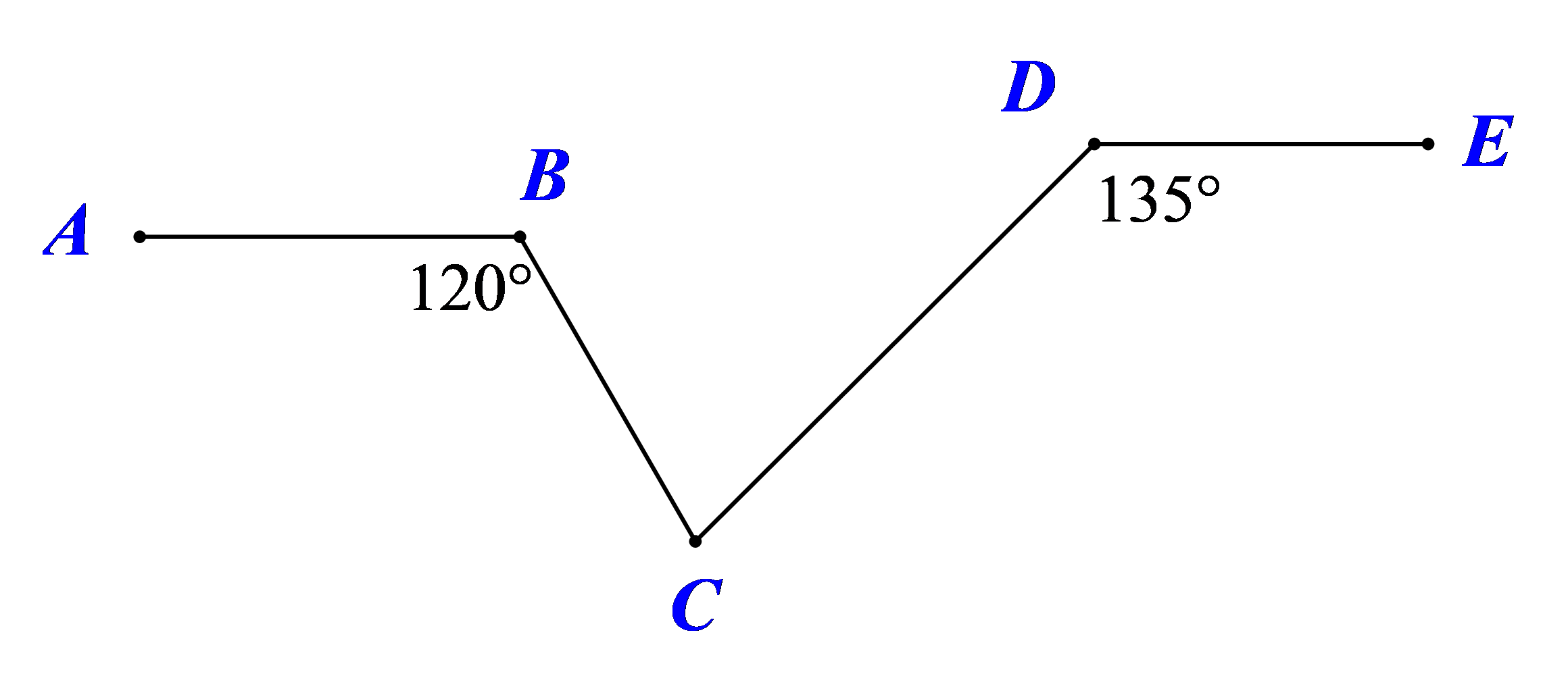
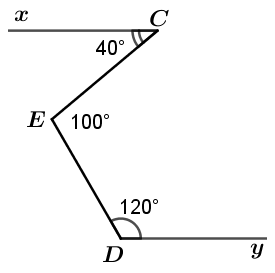
Kẻ đường thẳng qua \(C\) và song song với \[AB\].

Mà \(AB\,{\rm{//}}\,DE\) nên đường thẳng đó cũng song song với \[DE\].

Do đó \({\widehat C_1} + \widehat {ABC} = 180^\circ \) và \(\widehat {{C_2}} + \widehat {CDE} = 180^\circ \) (hai góc trong cùng phía)

Do đó, \[{\widehat C_1} = 60^\circ \] và \[\,{\widehat C_2} = 45^\circ \].

Suy ra \[\widehat {BCD} = 180^\circ - 60^\circ - 45^\circ = 75^\circ \].

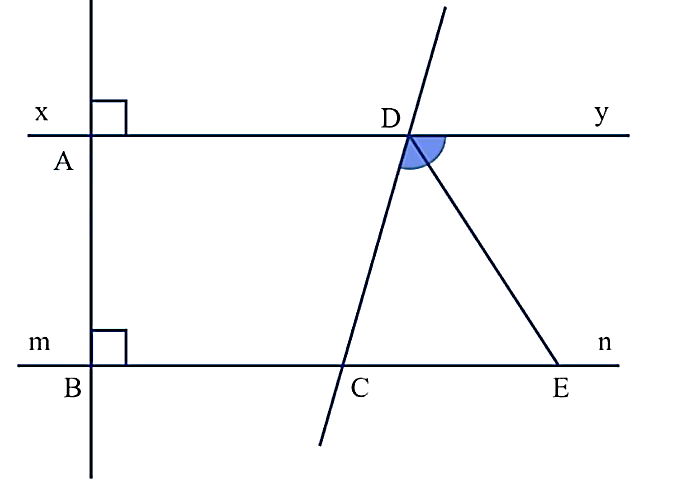
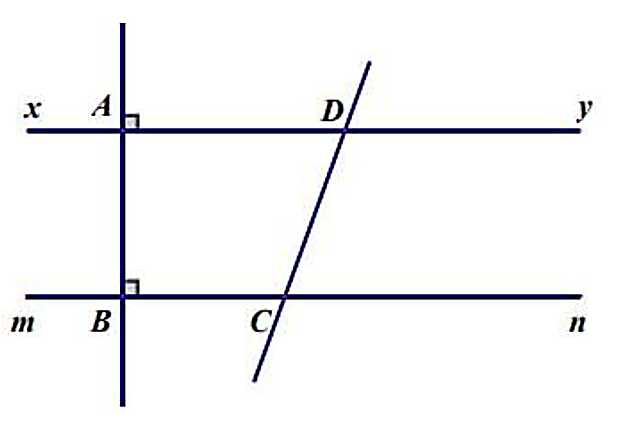
a) Ta có: \(xy \bot AB\) và \(mn \bot AB\) nên \(xy\parallel mn.\)

b) Ta có: \(\widehat {DCB} + \widehat {DCn} = 180^\circ \) (hai góc kề bù).

Suy ra \(\widehat {DCB} = 180^\circ - \widehat {DCn} = 180^\circ - 70^\circ = 110^\circ \).

Vì \(xy\parallel mn\) suy ra \(\widehat {DCB} = \widehat {CDy} = 110^\circ \) (hai góc so le trong).

c) Vì \(DE\) là tia phân giác của \(\widehat {CDy}\) nên \(\widehat {CDE} = \widehat {EDy} = \frac{{\widehat {CDy}}}{2} = \frac{{110^\circ }}{2} = 55^\circ \).

Vì \(xy\parallel mn\) suy ra \(\widehat {ECD} = \widehat {ADC} = 70^\circ \) (hai góc so le trong)

Mà \(\widehat {ADE} = \widehat {ADC} + \widehat {CDE} = 70^\circ + 55^\circ = 125^\circ \).