Biểu đồ dưới đây cho biết tỉ lệ các loại hoa nhập về của cửa hàng A trong một ngày
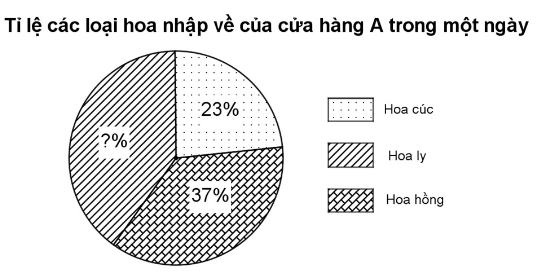
a) Tính tỉ lệ phần trăm của hoa ly nhập về trong cửa hàng và vẽ bảng thống kê biểu diễn biểu đồ trên.
b) Biết một ngày cửa hàng A nhập tổng cộng 2 000 bông. Tính số lượng hoa nhập về mỗi loại trong một ngày của cửa hàng A.
Biểu đồ dưới đây cho biết tỉ lệ các loại hoa nhập về của cửa hàng A trong một ngày
a) Tính tỉ lệ phần trăm của hoa ly nhập về trong cửa hàng và vẽ bảng thống kê biểu diễn biểu đồ trên.
b) Biết một ngày cửa hàng A nhập tổng cộng 2 000 bông. Tính số lượng hoa nhập về mỗi loại trong một ngày của cửa hàng A.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
a) Tỉ lệ phần trăm của hoa ly nhập về trong cửa hàng là: \(100 - 37 - 23 = 40\% \).
Ta có bảng thống kê tỉ lệ các loại hoa nhập ở cửa hàng A trong một ngày như sau:
|
Loại hoa |
Hoa hồng |
Hoa ly |
Hoa cúc |
|
Tỉ lệ phần trăm (%) |
37% |
40% |
23% |
b) Số lượng hoa hồng nhập về trong một ngày là: \(37\% .2000 = 740\) (bông).
Số lượng hoa ly nhập về trong một ngày là: \(40\% .2000 = 800\) (bông).
Số lượng hoa cúc nhập về trong một ngày là: \(2000 - 740 - 800 = 460\) (bông).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
a) Số tiền cả gốc và lãi mà bác Hoa thu được ở ngân hàng A sau một năm là:
\(70 \cdot 5,6\% + 70 = 73,92\) (triệu đồng)
Số tiền cả gốc và lãi bác Hoa thu được ở ngân hàng B sau một năm là:
\(50 \cdot 6,5\% + 50 = 53,25\) (triệu đồng)
Số tiền cả gốc và lãi mà bác Hoa thu được ở hai ngân hàng sau một năm là:
\(73,92 + 53,25 = 127,17\) (triệu đồng)
b) Số tiền cả gốc và lãi mà bác Hoa thu được ở một ngân hàng A ở năm thứ hai là:
\(\left( {73,92 - 73,92 \cdot 60\% } \right) \cdot 5,5\% - \left( {73,92 - 73,92 \cdot 60\% } \right) \approx 31,14\) (triệu đồng)
Số tiền cả gốc và lãi mà bác Hoa thu được ở ngân hàng B sau một năm là:
\(97,602 + 97,602 \cdot 6,8\% \approx 104,24\) (triệu đồng)
Số tiền cả gốc và lãi mà bác Hoa thu được ở hai ngân hàng sau hai năm là:
\(127,17 + 104,24 + 31,14 = 262,55\) (triệu đồng).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
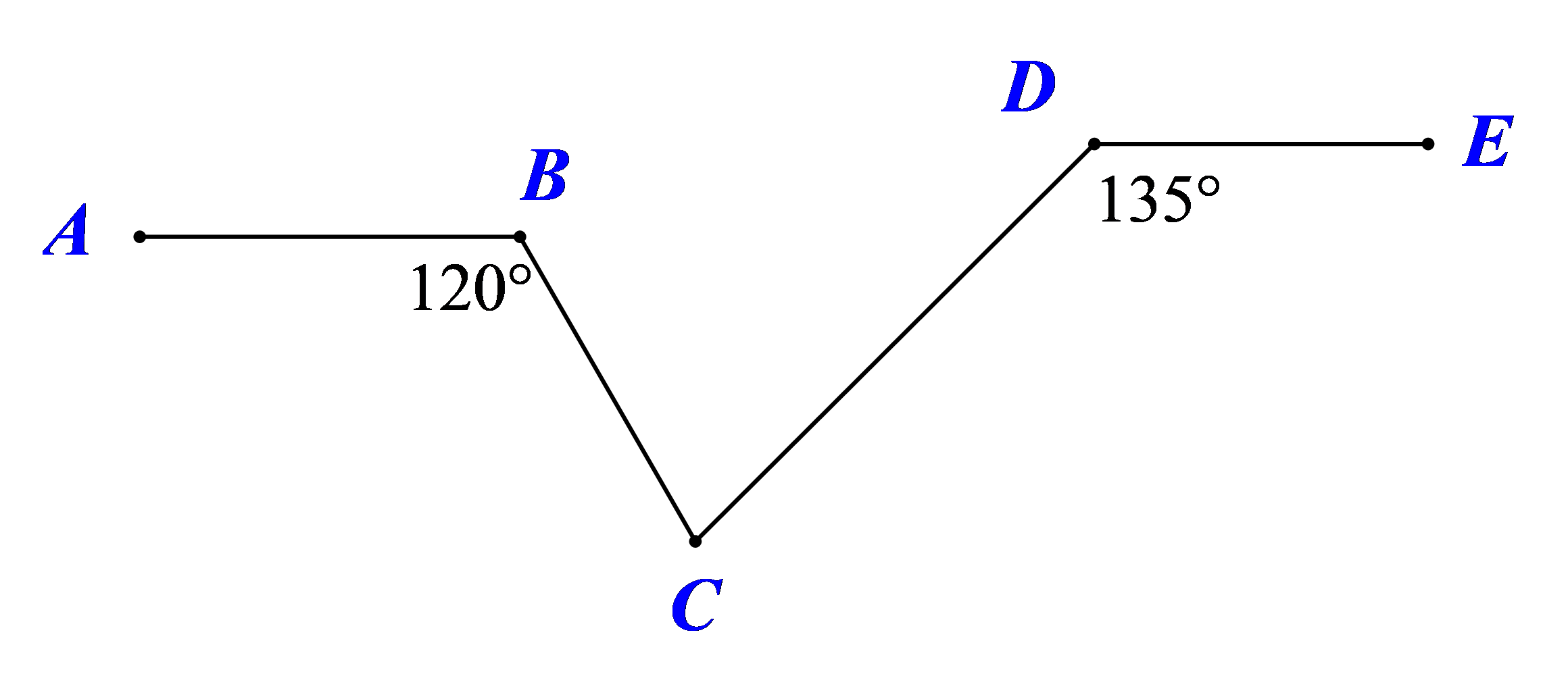
Kẻ đường thẳng qua \(C\) và song song với \[AB\].
Mà \(AB\,{\rm{//}}\,DE\) nên đường thẳng đó cũng song song với \[DE\].
Do đó \({\widehat C_1} + \widehat {ABC} = 180^\circ \) và \(\widehat {{C_2}} + \widehat {CDE} = 180^\circ \) (hai góc trong cùng phía)
Do đó, \[{\widehat C_1} = 60^\circ \] và \[\,{\widehat C_2} = 45^\circ \].
Suy ra \[\widehat {BCD} = 180^\circ - 60^\circ - 45^\circ = 75^\circ \].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập