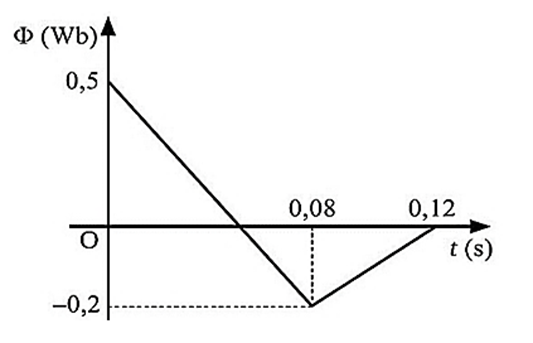
Một hạt neutron chậm bắn vào hạt nhân \(^{235}_{92}\text{U}\) đang đứng yên, gây ra phản ứng phân hạch theo phương trình:

\[
n + \,^{235}_{92}\text{U} \rightarrow \,^{90}_{36}\text{Kr} + \,^{144}_{56}\text{Ba} + x n
\]

Biết năng lượng liên kết riêng của \(^{235}_{92}\text{U}\) là \(7,60 \ \text{MeV/nucleon}\), của \(^{90}_{36}\text{Kr}\) là \(8,53 \ \text{MeV/nucleon}\) và của \(^{144}_{56}\text{Ba}\) là \(8,25 \ \text{MeV/nucleon}\).

Giá trị của \(x\) là bao nhiêu?

Từ thông gửi qua mặt giới hạn của một khung dây dẫn đặt trong từ trường có giá trị biến thiên theo thời gian được mô tả trong đồ thị ở hình bên dưới. Độ lớn cực đại suất điện động cảm ứng xuất hiện trong khung dây là bao nhiêu? (làm tròn kết quả đến chữ số phần trăm)

Khí carbon dioxide (CO$_2$) được sử dụng trong các bình chữa cháy. Khi mở van bình, do có sự chênh lệch về áp suất, CO$_2$ lỏng trong bình thoát ra ngoài qua hệ thống và chuyển thành dạng tuyết than khô (rắn), lạnh tới \(-78{,}5^\circ C\). Khi phun vào đám cháy, CO$_2$ có tác dụng làm loãng nồng độ hỗn hợp hơi khí cháy và làm lạnh vùng cháy, giúp dập tắt lửa. Để hoá lỏng CO$_2$ ở nhiệt độ \(20^\circ C\), cần áp suất tối thiểu về áp suất \(58 \, \text{atm}\). Muốn có một bình chứa \(4 \, \text{lít}\) CO$_2$ dạng lỏng ở nhiệt độ này phải cần ít nhất \(2200 \, \text{lít}\) khí CO$_2$ ở nhiệt độ \(20^\circ C\) và áp suất \(1 \, \text{atm}\).

a) Khí CO$_2$ được sử dụng trong bình chữa cháy nhờ khả năng làm lạnh và làm loãng hỗn hợp khí cháy.

b) Tuyết than khô là dạng CO$_2$ ở thể khí có nhiệt độ rất thấp.

c) Áp suất cần để hoá lỏng CO$_2$ ở \(20^\circ C\) là \(58 \, \text{atm}\).

d) Để tạo ra \(4 \, \text{lít}\) CO$_2$ lỏng, cần ít nhất \(2200 \, \text{lít}\) khí CO$_2$ ở \(20^\circ C\) và áp suất \(1 \, \text{atm}\).

Một học sinh thực hiện một thí nghiệm để tìm nhiệt hóa hơi riêng của nước. Một cốc thủy tinh chứa nước được đặt trên cân điện tử. Nước được đun nóng bằng một máy sưởi nhúng với công suất \(P = 100 \, W\), được nhúng trong nước sao cho không chạm vào cốc thủy tinh, như hình vẽ. Coi nhiệt lượng tỏa ra môi trường xung quanh không đáng kể. Cho nhiệt độ ban đầu của nước là \(27^\circ C\) và sôi ở \(100^\circ C\), nhiệt dung riêng của nước là \(4180 \, J/kg.K\). Khi nước bắt đầu sôi, học sinh đọc số cân. Sau 1,598 phút học sinh đọc lại số cân thu được kết quả như sau:

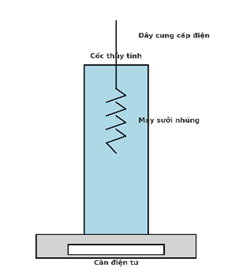
a) Khối lượng nước trong cốc giảm không đáng kể từ lúc bắt đầu đun đến khi nước bắt đầu sôi.

b) Năng lượng máy sưởi cung cấp trong 3 phút là \(18000 \, J\).

c) Nhiệt hóa hơi riêng của nước tính toán được là \(2{,}35 \cdot 10^6 \, J/kg\).

d) Nhiệt lượng cung cấp cho nước từ lúc bắt đầu đun cho đến thời gian \(3 \, \text{phút}\) là \(24000 \, J\).

Có 24 g khí lí tưởng chiếm thể tích \(5 \, \text{lít}\) ở \(27^\circ C\). Sau khi nung nóng đẳng áp khối lượng riêng của khí là \(2{,}5 \, g/l\). Tìm nhiệt độ của khí sau khi nung nóng theo đơn vị \(^\circ C\). (làm tròn kết quả đến hàng đơn vị).

Hình vẽ mô tả nguyên lý hoạt động của một chiếc bàn là hơi nước. Nước ban đầu từ bình ở nhiệt độ \(30^\circ C\) nhỏ xuống tấm kim loại, sau đó bay hơi thành hơi nước ở \(100^\circ C\). Bộ phận làm nóng có công suất điện là \(1{,}5 \, kW\). Giả sử toàn bộ năng lượng điện được truyền vào tấm kim loại, giúp duy trì nhiệt độ làm việc ổn định. Cho biết nhiệt dung riêng của nước là \(4180 \, J/kg.K\) và nhiệt hoá hơi riêng của nước là \(2{,}3 \cdot 10^6 \, J/kg\). Trong mỗi phút, bàn là tạo ra bao nhiêu gam hơi nước? (làm tròn kết quả đến phần trăm).

Một vật chuyển động thẳng đều đi được quãng đường S trong thời gian t. Tốc độ trung bình v của vật được tính theo công thức