4 bài tập Chủ đề 5. Chuyển động tròn đều có lời giải
27 người thi tuần này 4.6 689 lượt thi 4 câu hỏi 50 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử tốt nghiệp THPT môn Vật lí Sở Hòa Bình có đáp án
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Lê Quý Đôn (Hải Phòng) có đáp án
Đề thi thử tốt nghiệp THPT môn Vật lí Sở Yên Bái có đáp án
Đề thi thử tốt nghiệp THPT môn Vật lí Sở Thái Bình có đáp án
Đề thi thử tốt nghiệp THPT môn Vật lí Sở Lai Châu có đáp án
Đề thi thử tốt nghiệp THPT môn Vật lí Sở Bình Thuận có đáp án
Đề thi thử tốt nghiệp THPT môn Vật lý Cụm liên trường Ninh Bình có đáp án
Đề thi thử tốt nghiệp THPT môn Vật lý Sở Thanh Hóa có đáp án
Danh sách câu hỏi:
Lời giải
Tốc độ góc: \[\omega \] = 60 vòng/ phút = \[\frac{{60.2\pi }}{{60}} = 2\pi \,\left( {rad/s} \right)\]
Thời gian để hòn đá quay hết một vòng: \[T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{2\pi }} = 1\,s\]
Tốc độ: \[v = \omega r = 2\pi .1 = 6,28\,m/s\]
Lời giải
- Đối với kim giờ, chu kì của kim giờ là \[{T_h} = 12h = 43200\left( s \right)\] nên ta có:
\[\left\{ {\begin{array}{*{20}{c}}{{\omega _h} = \frac{{2\pi }}{{{T_h}}} \Rightarrow {\omega _h} = \frac{{2\pi }}{{43200}} \Rightarrow {\omega _h} \approx 1,{{454.10}^{ - 4}}\left( {rad/s} \right)}\\{{v_h} = {r_h}.\omega \Rightarrow {v_h} = 2,{{5.10}^{ - 2}}.1,{{45.10}^{ - 4}} \Rightarrow {v_h} \approx 3,{{635.10}^{ - 6}}\left( {m/s} \right)}\end{array}} \right.\]
- Đối với kim phút, chu kì của kim phút là \[{T_{ph}} = 60p = 3600\left( s \right)\] nên ta có:
\[\left\{ {\begin{array}{*{20}{c}}{{\omega _{ph}} = \frac{{2\pi }}{{{T_{ph}}}} \Rightarrow {\omega _{ph}} = \frac{{2\pi }}{{3600}} \Rightarrow {\omega _{ph}} \approx 1,{{745.10}^{ - 3}}\left( {rad/s} \right)}\\{{v_{ph}} = {r_{ph}}.\omega \Rightarrow {v_{ph}} = {{3.10}^{ - 2}}.1,{{745.10}^{ - 3}} \Rightarrow {v_{ph}} \approx 5,{{235.10}^{ - 5}}\left( {m/s} \right)}\end{array}} \right.\]
Ta có: \[\frac{{{\omega _h}}}{{{\omega _{ph}}}} = \frac{{1,{{454.10}^{ - 4}}}}{{1,{{745.10}^{ - 3}}}} \Rightarrow {\omega _{ph}} \approx 12{\omega _h}\]
Ta lại có: \[\frac{{{v_h}}}{{{v_{ph}}}} = \frac{{3,{{635.10}^{ - 6}}}}{{5,{{235.10}^{ - 5}}}} \Rightarrow {v_{ph}} \approx 14,4{v_h}\]
Lời giải
Lực hướng tâm: \[{F_{ht}} = m\frac{{{v^2}}}{R} = 12.\frac{{{8^2}}}{{0,4}} = 1920\,N\].
Lời giải
Hợp lực của áp lực và trọng lực đóng vai trò là lực hướng tâm: \[\overrightarrow {{F_{ht}}} = \overrightarrow P + \overrightarrow N \]
Khi ở điểm thấp nhất, áp lực hướng lên và ngược chiều trọng lực.
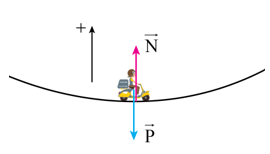
Chọn chiều dương hướng về tâm quay nên ta có: \[{F_{ht}} = - P + N \Leftrightarrow m\frac{{{v^2}}}{R} = - mg + N\]
\[ \Rightarrow N = m\left( {\frac{{{v^2}}}{R} + g} \right) = 95\left( {\frac{{{{15}^2}}}{{15}} + 10} \right) = 2375N\]