Câu hỏi:
23/12/2024 72
Để một vật có khối lượng bằng 12 kg chuyển động tròn đều trên quỹ đạo có bán kính 0,4 m với tốc độ 8 m/s thì lực hướng tâm phải có độ lớn gần nhất với giá trị nào?
Để một vật có khối lượng bằng 12 kg chuyển động tròn đều trên quỹ đạo có bán kính 0,4 m với tốc độ 8 m/s thì lực hướng tâm phải có độ lớn gần nhất với giá trị nào?
Câu hỏi trong đề: 4 bài tập Chủ đề 5. Chuyển động tròn đều có lời giải !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Lực hướng tâm: \[{F_{ht}} = m\frac{{{v^2}}}{R} = 12.\frac{{{8^2}}}{{0,4}} = 1920\,N\].
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
- Đối với kim giờ, chu kì của kim giờ là \[{T_h} = 12h = 43200\left( s \right)\] nên ta có:
\[\left\{ {\begin{array}{*{20}{c}}{{\omega _h} = \frac{{2\pi }}{{{T_h}}} \Rightarrow {\omega _h} = \frac{{2\pi }}{{43200}} \Rightarrow {\omega _h} \approx 1,{{454.10}^{ - 4}}\left( {rad/s} \right)}\\{{v_h} = {r_h}.\omega \Rightarrow {v_h} = 2,{{5.10}^{ - 2}}.1,{{45.10}^{ - 4}} \Rightarrow {v_h} \approx 3,{{635.10}^{ - 6}}\left( {m/s} \right)}\end{array}} \right.\]
- Đối với kim phút, chu kì của kim phút là \[{T_{ph}} = 60p = 3600\left( s \right)\] nên ta có:
\[\left\{ {\begin{array}{*{20}{c}}{{\omega _{ph}} = \frac{{2\pi }}{{{T_{ph}}}} \Rightarrow {\omega _{ph}} = \frac{{2\pi }}{{3600}} \Rightarrow {\omega _{ph}} \approx 1,{{745.10}^{ - 3}}\left( {rad/s} \right)}\\{{v_{ph}} = {r_{ph}}.\omega \Rightarrow {v_{ph}} = {{3.10}^{ - 2}}.1,{{745.10}^{ - 3}} \Rightarrow {v_{ph}} \approx 5,{{235.10}^{ - 5}}\left( {m/s} \right)}\end{array}} \right.\]
Ta có: \[\frac{{{\omega _h}}}{{{\omega _{ph}}}} = \frac{{1,{{454.10}^{ - 4}}}}{{1,{{745.10}^{ - 3}}}} \Rightarrow {\omega _{ph}} \approx 12{\omega _h}\]
Ta lại có: \[\frac{{{v_h}}}{{{v_{ph}}}} = \frac{{3,{{635.10}^{ - 6}}}}{{5,{{235.10}^{ - 5}}}} \Rightarrow {v_{ph}} \approx 14,4{v_h}\]
Lời giải
Hợp lực của áp lực và trọng lực đóng vai trò là lực hướng tâm: \[\overrightarrow {{F_{ht}}} = \overrightarrow P + \overrightarrow N \]
Khi ở điểm thấp nhất, áp lực hướng lên và ngược chiều trọng lực.
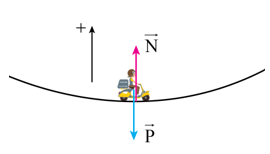
Chọn chiều dương hướng về tâm quay nên ta có: \[{F_{ht}} = - P + N \Leftrightarrow m\frac{{{v^2}}}{R} = - mg + N\]
\[ \Rightarrow N = m\left( {\frac{{{v^2}}}{R} + g} \right) = 95\left( {\frac{{{{15}^2}}}{{15}} + 10} \right) = 2375N\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi thử tốt nghiệp THPT môn Vật lí Sở Giáo dục và Đào tạo Nam Định có đáp án
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 3)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 4)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 2)
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 6)
-
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Yên Lạc - Vĩnh Phúc - Lần 1 có đáp án
-
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Trưng Yên - Hưng Yên có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận