Câu hỏi:
23/12/2024 92
Vòng xiếc là một vành tròn bán kính R = 15 m, nằm trong mặt phẳng thẳng đứng. Một người đi xe đạp trong vòng xiếc này, khối lượng cả xe và người là 95 kg. Lấy g = 10 m/s2. Biết tốc độ của xe không đổi là v = 15 m/s. Tính lực ép của xe lên vòng xiếc tại điểm thấp nhất.
Vòng xiếc là một vành tròn bán kính R = 15 m, nằm trong mặt phẳng thẳng đứng. Một người đi xe đạp trong vòng xiếc này, khối lượng cả xe và người là 95 kg. Lấy g = 10 m/s2. Biết tốc độ của xe không đổi là v = 15 m/s. Tính lực ép của xe lên vòng xiếc tại điểm thấp nhất.
Câu hỏi trong đề: 4 bài tập Chủ đề 5. Chuyển động tròn đều có lời giải !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hợp lực của áp lực và trọng lực đóng vai trò là lực hướng tâm: \[\overrightarrow {{F_{ht}}} = \overrightarrow P + \overrightarrow N \]
Khi ở điểm thấp nhất, áp lực hướng lên và ngược chiều trọng lực.
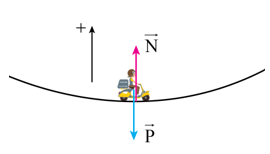
Chọn chiều dương hướng về tâm quay nên ta có: \[{F_{ht}} = - P + N \Leftrightarrow m\frac{{{v^2}}}{R} = - mg + N\]
\[ \Rightarrow N = m\left( {\frac{{{v^2}}}{R} + g} \right) = 95\left( {\frac{{{{15}^2}}}{{15}} + 10} \right) = 2375N\]
Hot: 500+ Đề thi thử tốt nghiệp THPT các môn, ĐGNL các trường ĐH... file word có đáp án (2025). Tải ngay
Sách thầy cô Vietjack biên soạn:
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- 500 Bài tập tổng ôn Vật lí (Form 2025) ( 38.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
Bình luận
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
- Đối với kim giờ, chu kì của kim giờ là \[{T_h} = 12h = 43200\left( s \right)\] nên ta có:
\[\left\{ {\begin{array}{*{20}{c}}{{\omega _h} = \frac{{2\pi }}{{{T_h}}} \Rightarrow {\omega _h} = \frac{{2\pi }}{{43200}} \Rightarrow {\omega _h} \approx 1,{{454.10}^{ - 4}}\left( {rad/s} \right)}\\{{v_h} = {r_h}.\omega \Rightarrow {v_h} = 2,{{5.10}^{ - 2}}.1,{{45.10}^{ - 4}} \Rightarrow {v_h} \approx 3,{{635.10}^{ - 6}}\left( {m/s} \right)}\end{array}} \right.\]
- Đối với kim phút, chu kì của kim phút là \[{T_{ph}} = 60p = 3600\left( s \right)\] nên ta có:
\[\left\{ {\begin{array}{*{20}{c}}{{\omega _{ph}} = \frac{{2\pi }}{{{T_{ph}}}} \Rightarrow {\omega _{ph}} = \frac{{2\pi }}{{3600}} \Rightarrow {\omega _{ph}} \approx 1,{{745.10}^{ - 3}}\left( {rad/s} \right)}\\{{v_{ph}} = {r_{ph}}.\omega \Rightarrow {v_{ph}} = {{3.10}^{ - 2}}.1,{{745.10}^{ - 3}} \Rightarrow {v_{ph}} \approx 5,{{235.10}^{ - 5}}\left( {m/s} \right)}\end{array}} \right.\]
Ta có: \[\frac{{{\omega _h}}}{{{\omega _{ph}}}} = \frac{{1,{{454.10}^{ - 4}}}}{{1,{{745.10}^{ - 3}}}} \Rightarrow {\omega _{ph}} \approx 12{\omega _h}\]
Ta lại có: \[\frac{{{v_h}}}{{{v_{ph}}}} = \frac{{3,{{635.10}^{ - 6}}}}{{5,{{235.10}^{ - 5}}}} \Rightarrow {v_{ph}} \approx 14,4{v_h}\]
Lời giải
Tốc độ góc: \[\omega \] = 60 vòng/ phút = \[\frac{{60.2\pi }}{{60}} = 2\pi \,\left( {rad/s} \right)\]
Thời gian để hòn đá quay hết một vòng: \[T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{2\pi }} = 1\,s\]
Tốc độ: \[v = \omega r = 2\pi .1 = 6,28\,m/s\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Đề thi HOT:
-
Đề thi thử tốt nghiệp THPT môn Vật lí Sở Giáo dục và Đào tạo Nam Định có đáp án
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 1)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 3)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 4)
-
Đề minh họa tốt nghiệp THPT môn Vật lý có đáp án năm 2025 (Đề 2)
-
(2025 mới) Đề ôn thi tốt nghiệp THPT Vật lí (Đề số 6)
-
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Yên Lạc - Vĩnh Phúc - Lần 1 có đáp án
-
Đề thi thử tốt nghiệp THPT môn Vật lí THPT Trưng Yên - Hưng Yên có đáp án
Hãy Đăng nhập hoặc Tạo tài khoản để gửi bình luận
-
-
Bình luận