Trong hình bên, bệnh nhân được cho chức năng thông khí phổi bằng phương pháp xạ hình phổi. Xạ hình phổi là phương pháp sử dụng một số đồng vị phóng xạ dạng khí hoặc dạng hơi hoặc dạng chất đánh dấu phóng xạ sử dụng dưới dạng khí dung \textit{aerosol} có kích thước hạt 0,1 – 0,5 \(\mu\)m. Sau khi cho người bệnh hít khí dùng phóng xạ, thuốc phóng xạ vào phổi, đi vào phế nang và lắng đọng ở đó với thời gian đủ dài để có thể ghi hình thông khí phổi từng vùng theo nhiều hướng. Dựa vào đó giúp bác sĩ đánh giá tình trạng thông khí phổi từng vùng và chẩn đoán một số bệnh về phổi.
Đồng vị phóng xạ xenon \(\,^{133}_{54}\text{Xe}\,\) được sử dụng phổ biến trong xạ hình phổi. Xenon \(\,^{133}\text{Xe}\,\) là chất phóng xạ \(\beta^-\) có chu kì bán rã là 5,24 ngày đêm. Một bệnh nhân được chỉ định sử dụng liều xenon có độ phóng xạ \(3{,}18\cdot 10^8\ \text{Bq}\). Coi rằng 85\% lượng xenon trong liều đó lắng đọng tại phổi. Bệnh nhân được chụp ảnh phổi lần thứ nhất ngay sau khi hít khí và lần thứ hai ngay sau đó 2 giờ. Biết khối lượng nguyên tử xenon là \(133\ \text{amu}\).
Hạt \(\beta^-\) được định hướng cho bay vào trong điện trường đều giữa hai bản kim loại phẳng song song, cách nhau một khoảng \(a=10\ \text{cm}\), dọc \(2a=20\ \text{cm}\); hiệu điện thế giữa hai bản là \(10\ \text{V}\) với vận tốc ban đầu \(v_0=2\cdot 10^6\ \text{m/s}\), theo phương song song với hai bản và gần sát bản âm. Bỏ qua trọng lực và các loại lực cản tác dụng lên hạt \(\beta^-\). Biết hạt \(\beta^-\) có điện tích \(q=-1{,}6\cdot 10^{-19}\ \text{C}\) và khối lượng \(m=9{,}1\cdot 10^{-31}\ \text{kg}\).
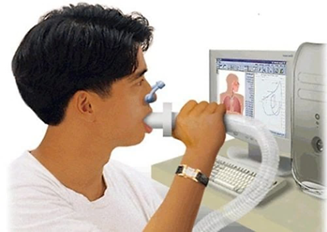
a) Hằng số phóng xạ của \(\,^{133}_{54}\text{Xe}\,\) là \(0{,}132\ \text{s}^{-1}\).
b) Khối lượng \(\,^{133}_{54}\text{Xe}\,\) có trong liều mà bệnh nhân đã hít vào xấp xỉ bằng \(0{,}046\ \mu\text{g}\).
c) Ở lần chụp thứ hai, lượng \(\,^{133}\text{Xe}\,\) đã lắng đọng tại phổi có độ phóng xạ xấp xỉ bằng \(3{,}15\cdot 10^{8}\ \text{Ci}\).
d) Tốc độ của hạt \(\beta^-\) khi đến bản dương xấp xỉ bằng \(2{,}74\cdot 10^{6}\ \text{m/s}\).
Trong hình bên, bệnh nhân được cho chức năng thông khí phổi bằng phương pháp xạ hình phổi. Xạ hình phổi là phương pháp sử dụng một số đồng vị phóng xạ dạng khí hoặc dạng hơi hoặc dạng chất đánh dấu phóng xạ sử dụng dưới dạng khí dung \textit{aerosol} có kích thước hạt 0,1 – 0,5 \(\mu\)m. Sau khi cho người bệnh hít khí dùng phóng xạ, thuốc phóng xạ vào phổi, đi vào phế nang và lắng đọng ở đó với thời gian đủ dài để có thể ghi hình thông khí phổi từng vùng theo nhiều hướng. Dựa vào đó giúp bác sĩ đánh giá tình trạng thông khí phổi từng vùng và chẩn đoán một số bệnh về phổi.
Đồng vị phóng xạ xenon \(\,^{133}_{54}\text{Xe}\,\) được sử dụng phổ biến trong xạ hình phổi. Xenon \(\,^{133}\text{Xe}\,\) là chất phóng xạ \(\beta^-\) có chu kì bán rã là 5,24 ngày đêm. Một bệnh nhân được chỉ định sử dụng liều xenon có độ phóng xạ \(3{,}18\cdot 10^8\ \text{Bq}\). Coi rằng 85\% lượng xenon trong liều đó lắng đọng tại phổi. Bệnh nhân được chụp ảnh phổi lần thứ nhất ngay sau khi hít khí và lần thứ hai ngay sau đó 2 giờ. Biết khối lượng nguyên tử xenon là \(133\ \text{amu}\).
Hạt \(\beta^-\) được định hướng cho bay vào trong điện trường đều giữa hai bản kim loại phẳng song song, cách nhau một khoảng \(a=10\ \text{cm}\), dọc \(2a=20\ \text{cm}\); hiệu điện thế giữa hai bản là \(10\ \text{V}\) với vận tốc ban đầu \(v_0=2\cdot 10^6\ \text{m/s}\), theo phương song song với hai bản và gần sát bản âm. Bỏ qua trọng lực và các loại lực cản tác dụng lên hạt \(\beta^-\). Biết hạt \(\beta^-\) có điện tích \(q=-1{,}6\cdot 10^{-19}\ \text{C}\) và khối lượng \(m=9{,}1\cdot 10^{-31}\ \text{kg}\).

a) Hằng số phóng xạ của \(\,^{133}_{54}\text{Xe}\,\) là \(0{,}132\ \text{s}^{-1}\).
b) Khối lượng \(\,^{133}_{54}\text{Xe}\,\) có trong liều mà bệnh nhân đã hít vào xấp xỉ bằng \(0{,}046\ \mu\text{g}\).
c) Ở lần chụp thứ hai, lượng \(\,^{133}\text{Xe}\,\) đã lắng đọng tại phổi có độ phóng xạ xấp xỉ bằng \(3{,}15\cdot 10^{8}\ \text{Ci}\).
d) Tốc độ của hạt \(\beta^-\) khi đến bản dương xấp xỉ bằng \(2{,}74\cdot 10^{6}\ \text{m/s}\).
Quảng cáo
Trả lời:
|
|
Nội dung |
Đúng |
Sai |
|
a |
Hằng số phóng xạ của \(\,^{133}_{54}\text{Xe}\,\) là \(0{,}132\ \text{s}^{-1}\). |
|
S |
|
b |
Khối lượng \(\,^{133}_{54}\text{Xe}\,\) có trong liều mà bệnh nhân đã hít vào xấp xỉ bằng \(0{,}046\ \mu\text{g}\). |
Đ |
|
|
c |
Ở lần chụp thứ hai, lượng \(\,^{133}\text{Xe}\,\) đã lắng đọng tại phổi có độ phóng xạ xấp xỉ bằng \(3{,}15\cdot 10^{8}\ \text{Ci}\).
|
|
S |
|
d |
Tốc độ của hạt \(\beta^-\) khi đến bản dương xấp xỉ bằng \(2{,}74\cdot 10^{6}\ \text{m/s}\). |
Đ |
|
a) SAI
Hằng số phóng xạ của \(\,^{133}_{54}\text{Xe}\,\):
\[
\lambda=\frac{\ln 2}{T}
=\frac{\ln 2}{5{,}24\cdot 24\cdot 3600}
\approx 0{,}1531\cdot 10^{-5}\ \text{s}^{-1}.
\]
b) ĐÚNG
Khối lượng \(\,^{133}\text{Xe}\,\) trong liều bệnh nhân đã hít vào:
\[
H_0=\lambda N_0,\qquad N_0=\frac{m_0}{M}N_A
\Rightarrow m_0=\frac{H_0\,T\,M}{\ln 2\,N_A}
=\frac{3{,}18\cdot 10^{8}\cdot 5{,}24\cdot 24\cdot 3600\cdot 133}{\ln 2\cdot 6{,}02\cdot 10^{23}}
\approx 0{,}046\cdot 10^{-6}\ \text{g}=0{,}046\ \mu\text{g}.
\]
c) SAI
Khối lượng \(\,^{133}\text{Xe}\,\) lắng đọng tại phổi: \(m_1=85\%\,m_0=0{,}85\,m_0\).
Độ phóng xạ tại thời điểm chụp thứ hai (sau \(t=2\ \text{h}\)):
\[
H=H_0\,2^{-t/T}=3{,}18\cdot 10^8\cdot 2^{-\,\frac{2}{5{,}24\cdot 24}}
\approx 3{,}15\cdot 10^{8}\ \text{Bq}.
\]
(Nên nhận xét ghi “Ci” là sai về đơn vị.)
d) ĐÚNG
Áp dụng định lí động năng:
\[
A_{\,\vec F_e}
=\frac12 m v^2-\frac12 m v_0^2
=q\,\vec E\cdot \vec d
=q\,U
\Rightarrow
v=\sqrt{\frac{2}{m}\,qU+v_0^2}
=\sqrt{\frac{2}{9{,}1\cdot 10^{-31}}\cdot(-1{,}6\cdot 10^{-19})\cdot(-10)+(2\cdot 10^{6})^2}
\approx 2{,}74\cdot 10^{6}\ \text{m/s}.
\]
(Vì hạt \(\beta^-\) chuyển động từ bản âm về phía bản dương nên \(qU>0\). Với \(U=Ed=-10\ \text{V}\) theo quy ước chiều \(E\) ngược hướng chuyển động điện tích âm.)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 20 đề thi tốt nghiệp môn Vật lí (có đáp án chi tiết) ( 38.000₫ )
- Sổ tay Vật lí 12 (chương trình mới) ( 18.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
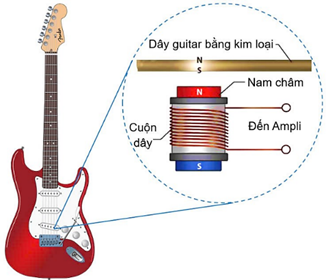
Suất điện động cảm ứng cực đại trong cuộn dây của bộ thu khi dây đàn dao động là:
\[
E_0 = N B S \omega = N B S \cdot 2\pi f.
\]
\[
E_0 = 310 \cdot 0{,}02 \cdot 5\cdot 10^{-4} \cdot 2\pi \cdot 500
\approx 9{,}7\ \text{V}.
\]
Lời giải
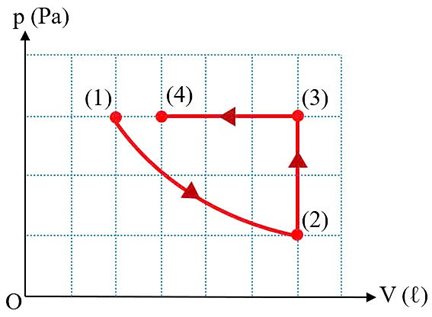
Từ trạng thái (1) sang trạng thái (2) là quá trình đẳng nhiệt nên
\[
T_2 = T_1 = 27 + 273 = 300\ \text{K}.
\]
Từ trạng thái (2) sang trạng thái (3) là quá trình đẳng tích, có áp suất tăng 3 lần nên nhiệt độ tuyệt đối tăng 3 lần. Khi đó:
\[
T_3 = 3T_2 = 3\cdot 300 = 900\ \text{K}.
\]
Từ trạng thái (3) sang trạng thái (4) là quá trình đẳng áp, có thể tích giảm 2 lần nên nhiệt độ tuyệt đối giảm 2 lần. Khi đó:
\[
T_4 = \frac{T_3}{2} = \frac{900}{2} = 450\ \text{K}.
\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(e_c = 0{,}5\pi \sin\!\left(100\pi t + \frac{\pi}{6}\right)\) (V).
B. \(e_c = -0{,}5\pi \cos\!\left(100\pi t + \frac{\pi}{6}\right)\) (V).
C. \(e_c = -50\pi \sin(100\pi t)\) (V).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 0,37 kg.
B. 0,67 kg.
C. 0,3 kg.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.