Biết \({}^{14}\text{C}\) là đồng vị phóng xạ \(\beta^-\) với chu kì bán rã là 5 730 năm (lấy 1 năm có 365 ngày). Một mẫu than nặng 5 g lấy từ một hố lửa cổ có độ phóng xạ C14 là 53,0 (phần rã/phút). Một cành cây còn sống có độ phóng xạ C14 là 15,3 (phần rã/phút) cho mỗi gram (g).
Biết \({}^{14}\text{C}\) là đồng vị phóng xạ \(\beta^-\) với chu kì bán rã là 5 730 năm (lấy 1 năm có 365 ngày). Một mẫu than nặng 5 g lấy từ một hố lửa cổ có độ phóng xạ C14 là 53,0 (phần rã/phút). Một cành cây còn sống có độ phóng xạ C14 là 15,3 (phần rã/phút) cho mỗi gram (g).
Hằng số phóng xạ của \({}^{14}\text{C}\) xấp xỉ bằng bao nhiêu p.s\(^{-1}\) (làm tròn kết quả đến hàng phần trăm)?
Quảng cáo
Trả lời:
\[
\lambda=\frac{\ln 2}{T}
=\frac{\ln 2}{5730\cdot 365\cdot 24\cdot 3600}
\approx 3{,}84\cdot 10^{-12}\ \text{s}^{-1}
=3{,}84\ \text{p.s}^{-1}.
\]
Câu hỏi cùng đoạn
Câu 2:
Tuổi của mẫu than lấy từ hố lửa cổ nói trên là bao nhiêu năm (làm tròn kết quả đến hàng trăm)?
Độ phóng xạ của mỗi gram C14 trong cây còn sống là: \(H_0 = 15{,}3\) (phần rã/phút).
Độ phóng xạ của mỗi gram C14 trong mẫu than:
\[
H=\frac{53{,}0}{5}=10{,}6\ \text{(phần rã/phút)}.
\]
Mà: \(H=H_0\cdot 2^{-t/T}\ \Rightarrow\ \frac{H_0}{H}=2^{t/T}\ \Rightarrow\ t=T\cdot\log_2\!\left(\frac{H_0}{H}\right).\)
\[
t=5730\cdot \log_2\!\left(\frac{15{,}3}{10{,}6}\right)\approx 3000\ \text{năm}.
\]
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 1000 câu hỏi lí thuyết môn Vật lí (Form 2025) ( 45.000₫ )
- 500 Bài tập tổng ôn Vật lí (Form 2025) ( 38.000₫ )
- Bộ đề thi tốt nghiệp 2025 các môn Toán, Lí, Hóa, Văn, Anh, Sinh, Sử, Địa, KTPL (có đáp án chi tiết) ( 36.000₫ )
- Tổng ôn lớp 12 môn Toán, Lí, Hóa, Văn, Anh, Sinh Sử, Địa, KTPL (Form 2025) ( 36.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
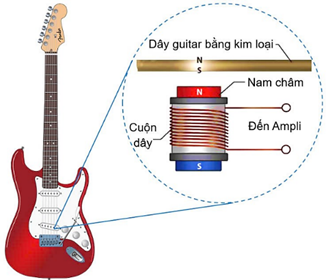
Suất điện động cảm ứng cực đại trong cuộn dây của bộ thu khi dây đàn dao động là:
\[
E_0 = N B S \omega = N B S \cdot 2\pi f.
\]
\[
E_0 = 310 \cdot 0{,}02 \cdot 5\cdot 10^{-4} \cdot 2\pi \cdot 500
\approx 9{,}7\ \text{V}.
\]
Lời giải
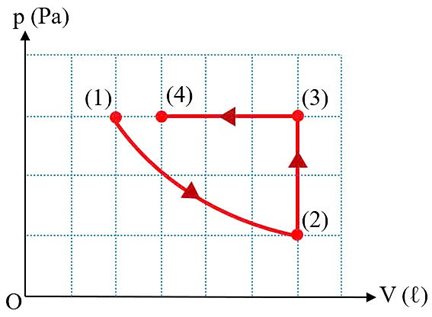
Từ trạng thái (1) sang trạng thái (2) là quá trình đẳng nhiệt nên
\[
T_2 = T_1 = 27 + 273 = 300\ \text{K}.
\]
Từ trạng thái (2) sang trạng thái (3) là quá trình đẳng tích, có áp suất tăng 3 lần nên nhiệt độ tuyệt đối tăng 3 lần. Khi đó:
\[
T_3 = 3T_2 = 3\cdot 300 = 900\ \text{K}.
\]
Từ trạng thái (3) sang trạng thái (4) là quá trình đẳng áp, có thể tích giảm 2 lần nên nhiệt độ tuyệt đối giảm 2 lần. Khi đó:
\[
T_4 = \frac{T_3}{2} = \frac{900}{2} = 450\ \text{K}.
\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(e_c = 0{,}5\pi \sin\!\left(100\pi t + \frac{\pi}{6}\right)\) (V).
B. \(e_c = -0{,}5\pi \cos\!\left(100\pi t + \frac{\pi}{6}\right)\) (V).
C. \(e_c = -50\pi \sin(100\pi t)\) (V).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
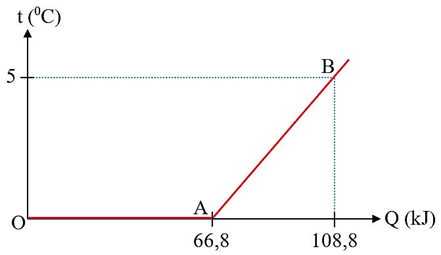
Câu 6
A. 0,37 kg.
B. 0,67 kg.
C. 0,3 kg.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.